题目内容
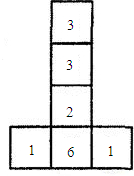六个面上分别标有1，1，2，3，3，6六个数字的均匀立方体的表面展开图如图所示，掷这个立方体一次，记朝上一面的数为平面直角坐标系中某个点的横坐标，朝下一面的数为该点的纵坐标．按照这样的规定，每掷一次该小立方体，就得到平面内一个点的坐标．求：（1）投掷这样的立方体得到点的坐标为（1，1）的概率；
（2）投掷这样的立方体得到的点在坐标平面内能位于直线y=x上方的概率．
分析：根据随机事件概率大小的求法，找准两点：
①、符合条件的情况数目；
②、全部情况的总数．
二者的比值就是其发生的概率的大小．
①、符合条件的情况数目；
②、全部情况的总数．
二者的比值就是其发生的概率的大小．
解答：解：（1）每掷一次可能得到的六个点的坐标分别是（1，1）、（1，1）、（2，3）、（3，2）
（3，6）、（6、3），
所以得到（1，1）的概率为
；
（2）由（1）知，位于直线y=x上方的点是（2，3）和（3，6），
所以位于直线y上方的点的概率是
．
（3，6）、（6、3），
所以得到（1，1）的概率为
| 1 |
| 3 |
（2）由（1）知，位于直线y=x上方的点是（2，3）和（3，6），
所以位于直线y上方的点的概率是
| 1 |
| 3 |
点评：用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
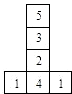六个面上分别标有1，1，2，3，4，5六个数字的均匀立方体的表现展开图如图所示，掷这个立方体一次，记朝上一面的数为平面直角坐标系中某个点的横坐标，朝下一面的数为该点的纵坐标．则得到的坐标落在抛物线y=2x2-x上的概率是（ ）