题目内容
如图，BC为⊙O内一条弦，直径AD垂直BC于点E，连接AB、CD，若BC=8，AD=10，则CD的长为（ ）分析：连接OB，根据垂径定理求出BE=CE=4，根据勾股定理求出OE，求出DE，在△DEC中，根据勾股定理求出DC即可．
解答：解：
连接OB，
∵直径AD⊥BC，
∴BE=CE=
BC=4，
∵直径AD=10，
∴OB=OD=5，
在Rt△BEO中，由勾股定理得：OE=
=
=3，
∴ED=5-3=2，
在Rt△CEO中，由勾股定理得：DC=
=
=2
，
故选D．
连接OB，
∵直径AD⊥BC，
∴BE=CE=
| 1 |
| 2 |
∵直径AD=10，
∴OB=OD=5，
在Rt△BEO中，由勾股定理得：OE=
| OB2-BE2 |
| 52-42 |
∴ED=5-3=2，
在Rt△CEO中，由勾股定理得：DC=
| CE2+ED2 |
| 42+22 |
| 5 |
故选D．
点评：本题考查了勾股定理和垂径定理，关键是求出各个线段的长度，构造直角三角形是有关应用垂径定理经常作的辅助线．
练习册系列答案
优生乐园系列答案
相关题目
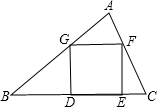如图，在△ABC中有一内接正方形DEFG，BC=a，BC上的高为h，则正方形DEFG的边长是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
（2013•邯郸一模）如图，D为△ABC内一点，CD平分∠ACB，BE⊥CD，垂足为D，交AC于点E，∠A=∠ABE．若AC=5，BC=3，则BD的长为（ ）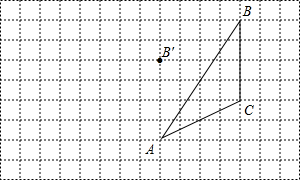
如图，在方格纸内将△ABC经过一次平移后得到△A′B′C′，图中标出了点A的对应点A'．
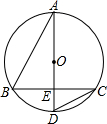如图，BC为⊙O内一条弦，直径AD垂直BC于点E，连接AB、CD，若BC=8，AD=10，则CD的长为
