Question

【题目】已知抛物线l1经过点E（1，0）和F（5，0），并交y轴于D（0，﹣5）；抛物线l2：y=ax2﹣（2a+2）x+3（a≠0），
（1）试求抛物线l1的函数解析式；
（2）求证：抛物线 l2与x轴一定有两个不同的交点；
（3）若a=1，抛物线l1、l2顶点分别为、；当x的取值范围是时，抛物线l1、l2 上的点的纵坐标同时随横坐标增大而增大；
（4）若a=1，已知直线MN分别与x轴、l1、l2分别交于点P（m，0）、M、N，且MN∥y轴，当1≤m≤5时，求线段MN的最大值．

Answer 1

【答案】
（1）

解：∵抛物线l1过E、F，

∴可设l1的解析式为y=a′（x﹣1）（x﹣5），

∵当x=0，y=﹣5，

∴﹣5=a′（﹣1）×（﹣5），

∴a′=﹣1，

∴y=﹣（x﹣1）（x﹣5）=﹣x2+6x﹣5

（2）

解：在y=ax2﹣（2a+2）x+3中，令y=0可得ax2﹣（2a+2）x+3=0，

∵△=（2a+2）2﹣4a×3=4（a﹣ ）2+3＞0，

∴抛物线l2与x轴一定有两个不同的交点

（3）（3，4）；（2，﹣1）；2≤x≤3
（4）

联立两抛物线解析式可得 ，解得 或 ，

∴l1、l2的两交点坐标为（1，0）和（4，3），且抛物线l1与x轴交于点（1，0）和（5，0），

∵直线MN分别与x轴、l1、l2分别交于点P（m，0）、M、N，且MN∥y轴，

∴M（m，﹣m2+6m﹣5），N（m，m2﹣4m+3），

当1≤m≤4时，如图1，

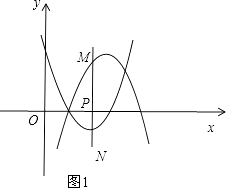
则MN=﹣m2+6m﹣5﹣（m2﹣4m+3）=﹣2m2+10m﹣8=﹣2（x﹣ ）2+ ，

∵﹣2＜0，

∴当m= 时，MN有最大值 ；

当4＜m≤5时，如图2，

则MN=m2﹣4m+3﹣（﹣m2+6m﹣5）=2m2﹣10m+8，

∵MN=2m2﹣10m+8有最小值，但在对称轴右边MN随x增大而增大，

∴当m=5时，MN最大=2×25﹣50+8=8，

综合可知当1≤m≤5时，MN最大值为8

【解析】（3）解：当a=1时，
∵抛物线l1的解析式为y=﹣x2+6x﹣5=﹣（x﹣3）2+4，抛物线l2的解析式为y=x2﹣4x+3=（x﹣2）2﹣1，
∴l1、l2的顶点分别为（3，4）、（2，﹣1），
∵﹣1＜0，1＞0，
∴抛物线l1开口向下，当x≤3时，y随x的增大而增大，抛物线l2开口向上，当x≥2时，y随x的增大而增大，
∴当2≤x≤3时，抛物线l1、l2上的点的纵坐标同时随横坐标增大而增大；
所以答案是：（3，4）；（2，﹣1）；2≤x≤3；
【考点精析】本题主要考查了二次函数的性质的相关知识点，需要掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能正确解答此题．