题目内容
(1)一只不透明的袋子中装有颜色分别为红、黄、蓝、白的球各1个.这些球除颜色外都相同.求下列事件的概率:①搅匀后从中任意摸出1个球,恰好是红球;
②搅匀后从中任意摸出1个球,记录下颜色后放回袋子中并搅匀,再从中任意摸出1个球,两次都是红球;
(2)某次考试共有6道选择题,每道题所给出的4个选项中,恰有一个是正确的.如果小明从每道题的4个选项中随机地选择1个,那么他6道选择题全部正确的概率是______.
A.
 B.
B.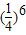 C.1-
C.1-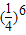 D.1-
D.1- .
.
【答案】分析:(1)①搅匀后从4个球中任意摸出1个球,求出恰好是红球的概率即可;
②列表得出所有等可能的情况数,找出两次都是红球的情况数,即可求出所求的概率;
(2)求出每一道题选择正确的概率,利用乘法法则即可求出全部正确的概率.
解答:解:(1)①搅匀后从中任意摸出1个球,恰好是红球的概率为 ;
;
②列表如下:
所有等可能的情况数有16种,其中两次都为红球的情况数有1种,
则P= ;
;
(2)每道题所给出的4个选项中,恰有一个是正确的概率为 ,
,
则他6道选择题全部正确的概率是( )6.
)6.
故选B.
点评:此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.
②列表得出所有等可能的情况数,找出两次都是红球的情况数,即可求出所求的概率;
(2)求出每一道题选择正确的概率,利用乘法法则即可求出全部正确的概率.
解答:解:(1)①搅匀后从中任意摸出1个球,恰好是红球的概率为
 ;
;②列表如下:
| 红 | 黄 | 蓝 | 绿 | |
| 红 | (红,红) | (黄,红) | (蓝,红) | (绿,红) |
| 黄 | (红,黄) | (黄,黄) | (蓝,黄) | (绿,黄) |
| 蓝 | (红,蓝) | (黄,蓝) | (蓝,蓝) | (绿,蓝) |
| 绿 | (红,绿) | (黄,绿) | (蓝,绿) | (绿,绿) |
则P=
 ;
;(2)每道题所给出的4个选项中,恰有一个是正确的概率为
 ,
,则他6道选择题全部正确的概率是(
 )6.
)6.故选B.
点评:此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
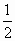 ,可以怎样向袋中放球?
,可以怎样向袋中放球?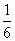 ,可以怎样向袋中放球?
,可以怎样向袋中放球?