题目内容
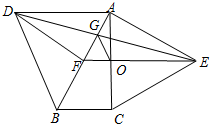 如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,连接DF、EF、DE,EF与AC交于点O,DE与AB交于点G,连接OG,若∠BAC=30°,下列结论:①△DBF≌△EFA;②AD=AE;③EF⊥AC;④AD=4AG;⑤△AOG与△EOG的面积比为1:4.
如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,连接DF、EF、DE,EF与AC交于点O,DE与AB交于点G,连接OG,若∠BAC=30°,下列结论:①△DBF≌△EFA;②AD=AE;③EF⊥AC;④AD=4AG;⑤△AOG与△EOG的面积比为1:4.
其中正确结论的个数是
- A.2个
- B.3个
- C.4个
- D.5个
B
分析:根据等边三角形的性质和已知先证△ABC≌△EFA,判断出③正确;再证△DBF≌△EFA,判断出①②;根据含30度角的直角三角形性质即可判断出④,根据三角形的面积和等高的三角形的面积比等于对应的边之比即可求出△AOG与△EOG的面积比为1:3,即可判断出⑤.
解答:解∵△ACE是等边三角形
∴∠EAC=60°,AE=AC,
∵∠BAC=30°,
∴∠FAE=∠ACB=90°,AB=2BC
∵F为AB的中点,
∴AB=2AF,
∴BC=AF,
∴△ABC≌△EFA,
∴∠AEF=∠BAC=30°,
∴∠AOE=180°-30°-60°=90°,∴③正确;
∵AD=BD,BF=AF,
∴∠DFB=90°,∠BDF=30°,
∵∠FAE=∠BAC+∠CAE=90°,
∴∠DFB=∠EAF,
∵EF⊥AC,
∴∠AEF=30°,
∴∠BDF=∠AEF,
∴△DBF≌△EFA(AAS),∴①正确;
∵△DBF≌△EFA,
∴AE=DF,
在Rt△ADF中,斜边AD>直角边DF,
即AD>AE,∴②错误;
∵△ADB是等边三角形,
∴AD=DB,∠ADB=60°,
∵F为AB中点,
∴∠ADF=30°,
∴AD=2AF,
∵△BDF≌△FAE,
∴AE=DF,EF=BD=AD,
∴四边形DFEA是平行四边形,
∴AF=2AG=2FG,
∴AD=2AF=4AG,∴④正确;
设OF=a,
∵EF⊥AC,
∴∠AOF=90°,
∵∠CAB=30°,
∴AF=2a,
∵∠AFO=∠AFO,∠AOF=∠FAE=90°,
∴△FAO∽△FEA,
∴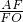 =
= ,
,
∴ =
=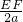 ,
,
∴EF=4a,
∴EO=4a-a=3a,
∵△FGO的边FO上的高和△EOG的边EO上的高相等,
∴S△EOG=3S△FOG,
∵AG=GF,△AOG的边AG上的高和△FOG的边FG上的高相等,
∴S△AOG=S△FOG,
即△AOG与△EOG的面积比为1:3,∴⑤错误;
故选B.
点评:本题考查了全等三角形的性质和判定,对应三角形的性质和判定,等边三角形的性质,三角形的面积,相似三角形的性质和判定,含30度角的直角三角形性质,平行四边形的性质和判定等知识点的综合运用.
分析:根据等边三角形的性质和已知先证△ABC≌△EFA,判断出③正确;再证△DBF≌△EFA,判断出①②;根据含30度角的直角三角形性质即可判断出④,根据三角形的面积和等高的三角形的面积比等于对应的边之比即可求出△AOG与△EOG的面积比为1:3,即可判断出⑤.
解答:解∵△ACE是等边三角形
∴∠EAC=60°,AE=AC,
∵∠BAC=30°,
∴∠FAE=∠ACB=90°,AB=2BC
∵F为AB的中点,
∴AB=2AF,
∴BC=AF,
∴△ABC≌△EFA,
∴∠AEF=∠BAC=30°,
∴∠AOE=180°-30°-60°=90°,∴③正确;
∵AD=BD,BF=AF,
∴∠DFB=90°,∠BDF=30°,
∵∠FAE=∠BAC+∠CAE=90°,
∴∠DFB=∠EAF,
∵EF⊥AC,
∴∠AEF=30°,
∴∠BDF=∠AEF,
∴△DBF≌△EFA(AAS),∴①正确;
∵△DBF≌△EFA,
∴AE=DF,
在Rt△ADF中,斜边AD>直角边DF,
即AD>AE,∴②错误;
∵△ADB是等边三角形,
∴AD=DB,∠ADB=60°,
∵F为AB中点,
∴∠ADF=30°,
∴AD=2AF,
∵△BDF≌△FAE,
∴AE=DF,EF=BD=AD,
∴四边形DFEA是平行四边形,
∴AF=2AG=2FG,
∴AD=2AF=4AG,∴④正确;
设OF=a,
∵EF⊥AC,
∴∠AOF=90°,
∵∠CAB=30°,
∴AF=2a,
∵∠AFO=∠AFO,∠AOF=∠FAE=90°,
∴△FAO∽△FEA,
∴
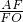 =
= ,
,∴
 =
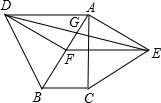
=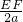 ,
,∴EF=4a,
∴EO=4a-a=3a,
∵△FGO的边FO上的高和△EOG的边EO上的高相等,
∴S△EOG=3S△FOG,
∵AG=GF,△AOG的边AG上的高和△FOG的边FG上的高相等,
∴S△AOG=S△FOG,
即△AOG与△EOG的面积比为1:3,∴⑤错误;
故选B.
点评:本题考查了全等三角形的性质和判定,对应三角形的性质和判定,等边三角形的性质,三角形的面积,相似三角形的性质和判定,含30度角的直角三角形性质,平行四边形的性质和判定等知识点的综合运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为平行四边形;③AD=4AG;④△DBF≌△EFA.其中正确结论的序号是
如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为平行四边形;③AD=4AG;④△DBF≌△EFA.其中正确结论的序号是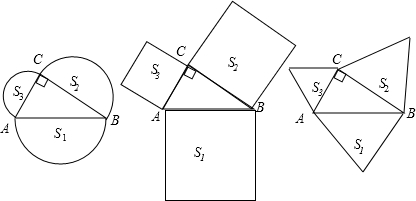
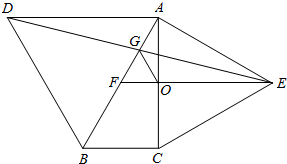 如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,连接DF、EF、DE,EF与AC交于点O,DE与AB交于点G,连接OG,若∠BAC=30°,下列结论:
如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,连接DF、EF、DE,EF与AC交于点O,DE与AB交于点G,连接OG,若∠BAC=30°,下列结论: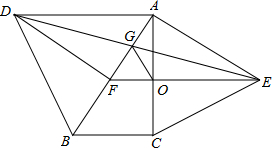 如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB中点,连接DF、EF,DE、EF与AC交于点O,DE与AB交于点G,连接OG,若∠BAC=30°,下列结论:①△DBF≌△EFA;②AD=AE;③EF⊥AC;④AD=4AG;⑤△AOG与△EOG的面积比为1:4.其中正确的结论的序号是
如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB中点,连接DF、EF,DE、EF与AC交于点O,DE与AB交于点G,连接OG,若∠BAC=30°,下列结论:①△DBF≌△EFA;②AD=AE;③EF⊥AC;④AD=4AG;⑤△AOG与△EOG的面积比为1:4.其中正确的结论的序号是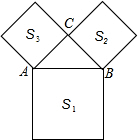 如图,分别以Rt△ABC三边为边向外作三个正方形,其面积分别用S1、S2、S3表示,容易得出S1、S2、S3之间有的关系式
如图,分别以Rt△ABC三边为边向外作三个正方形,其面积分别用S1、S2、S3表示,容易得出S1、S2、S3之间有的关系式