题目内容
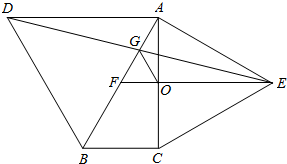 如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,连接DF、EF、DE,EF与AC交于点O,DE与AB交于点G,连接OG,若∠BAC=30°,下列结论:
如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,连接DF、EF、DE,EF与AC交于点O,DE与AB交于点G,连接OG,若∠BAC=30°,下列结论:①△DBF≌△EFA;②AD=AE;③EF⊥AC;④AD=4AG;⑤△AOG与△EOG的面积比为1:4.
其中正确结论的序号是( )
| A、①②③ | B、①④⑤ | C、①③⑤ | D、①③④ |
分析:若∠BAC=30°,
AB=2AC,由于△ABD、△ACE都是等边三角形,显然AD≠AE,而△DBF和△EFA中,∠DBF=∠AFO=60°,易证得∠FAE、∠DFB都是直角,且F是AB中点,由此证得两个三角形全等,可得DF=EA,进而可证得△DFG≌△AGE,即AF=2AG,AD=4AG,运用排除法即可得到D选项是正确的.
| 3 |
解答: 解:Rt△ABC中,若∠BAC=30°,设BC=2,则AC=2
解:Rt△ABC中,若∠BAC=30°,设BC=2,则AC=2
,AB=4;
∴AF=2,AE=2
,
∵∠BAC+∠OAE=30°+60°=90°,即△EFA是直角三角形,
∴tan∠AEF=
=
,即∠AEF=30°,EF平分∠AEC,
根据等边三角形三线合一的性质知:EF⊥AC,且O是AC的中点;(故③正确)
①∵F是AB的中点,∴AF=BF;
根据等边三角形三线合一的性质知:DF⊥AB,
∵∠BAC=30°,
∴∠AFO=90°-∠BAC=60°,即∠DBF=∠AFE=60°;
∵∠FAE=30°+60°=90°=∠BFD,
∴△DBF≌△EFA,故①正确;
②在Rt△ABC中,AB>AC,
∵AB=AD,AC=AE,
∴AD>AE,故②错误;
④由①的全等三角形知:DF=EA,
又∵∠DFG=∠EAG=90°,∠DGF=∠EGA,
∴△DFG≌△EAG,即AG=GF,
∴AD=2AF=4AG,故④正确;
⑤由④知:G是AF中点,由已知设AB=4,可以求出:EO=3,AO=
,
∴S△EOG=
OE•(
OA)=
×3×
=
;
又S△AOG=
AG•AO•sin30°=
×1×
=
,
故△AOG与△EOG的面积比为1:3,故⑤错误;
因此正确的结论是:①③④,
故选:D.
 解:Rt△ABC中,若∠BAC=30°,设BC=2,则AC=2
解:Rt△ABC中,若∠BAC=30°,设BC=2,则AC=2| 3 |
∴AF=2,AE=2
| 3 |
∵∠BAC+∠OAE=30°+60°=90°,即△EFA是直角三角形,
∴tan∠AEF=
| AF |
| AE |
| ||
| 3 |
根据等边三角形三线合一的性质知:EF⊥AC,且O是AC的中点;(故③正确)
①∵F是AB的中点,∴AF=BF;
根据等边三角形三线合一的性质知:DF⊥AB,
∵∠BAC=30°,
∴∠AFO=90°-∠BAC=60°,即∠DBF=∠AFE=60°;
∵∠FAE=30°+60°=90°=∠BFD,
∴△DBF≌△EFA,故①正确;
②在Rt△ABC中,AB>AC,
∵AB=AD,AC=AE,
∴AD>AE,故②错误;
④由①的全等三角形知:DF=EA,
又∵∠DFG=∠EAG=90°,∠DGF=∠EGA,
∴△DFG≌△EAG,即AG=GF,
∴AD=2AF=4AG,故④正确;
⑤由④知:G是AF中点,由已知设AB=4,可以求出:EO=3,AO=
| 3 |
∴S△EOG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
3
| ||
| 4 |
又S△AOG=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
故△AOG与△EOG的面积比为1:3,故⑤错误;
因此正确的结论是:①③④,
故选:D.
点评:此题主要考查的是直角三角形、等边三角形的性质、全等三角形的判定以及图形面积的求法,难度适中.

练习册系列答案
相关题目
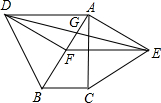 如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为平行四边形;③AD=4AG;④△DBF≌△EFA.其中正确结论的序号是
如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为平行四边形;③AD=4AG;④△DBF≌△EFA.其中正确结论的序号是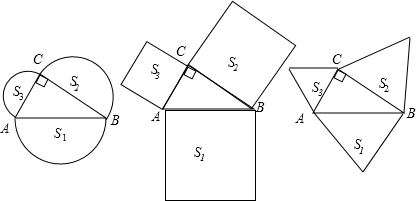
 如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB中点,连接DF、EF,DE、EF与AC交于点O,DE与AB交于点G,连接OG,若∠BAC=30°,下列结论:①△DBF≌△EFA;②AD=AE;③EF⊥AC;④AD=4AG;⑤△AOG与△EOG的面积比为1:4.其中正确的结论的序号是
如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB中点,连接DF、EF,DE、EF与AC交于点O,DE与AB交于点G,连接OG,若∠BAC=30°,下列结论:①△DBF≌△EFA;②AD=AE;③EF⊥AC;④AD=4AG;⑤△AOG与△EOG的面积比为1:4.其中正确的结论的序号是 如图,分别以Rt△ABC三边为边向外作三个正方形,其面积分别用S1、S2、S3表示,容易得出S1、S2、S3之间有的关系式
如图,分别以Rt△ABC三边为边向外作三个正方形,其面积分别用S1、S2、S3表示,容易得出S1、S2、S3之间有的关系式