题目内容
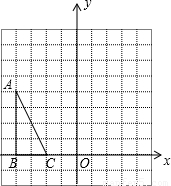
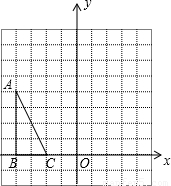
 已知:△ABC在直角坐标系中,A(-4,4),B(-4,0),C(-2,0)
已知:△ABC在直角坐标系中,A(-4,4),B(-4,0),C(-2,0)(1)将△ABC沿y轴翻折得到△DEF,画出△DEF,并写出点D的坐标
(4,4)
(4,4)
.(2)将△ABC绕原点O顺时针旋转90°得到△PMN,画出△PMN,并写出点P的坐标
(4,4)
(4,4)
.(3)△DEF与△PMN关于直线
y=x
y=x
对称.分析:(1)D与A关于y轴对称,据此即可确定D的坐标;
(2)B,C旋转以后的对应点一定在y轴的正半轴上,即可确定位置,然后过M作y轴的垂线,截取MP=AB即可确定P的位置;
(3)根据作图即可确定对称的直线.
(2)B,C旋转以后的对应点一定在y轴的正半轴上,即可确定位置,然后过M作y轴的垂线,截取MP=AB即可确定P的位置;
(3)根据作图即可确定对称的直线.
解答:解:(1)D的坐标是:(-4,4)关于y轴的对称点,则坐标是(4,4);
(2)P的坐标是:(4,4);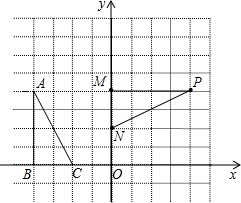
(3)△DEF与△PMN关于直线y=x对称.
(2)P的坐标是:(4,4);

(3)△DEF与△PMN关于直线y=x对称.
点评:本题考查旋转变换作图,在找旋转中心时,要抓住“动”与“不动”,看图是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目