题目内容
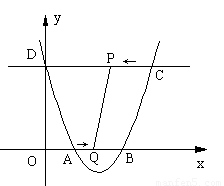
如图,已知抛物线y=x![]() -ax+a
-ax+a![]() -4a-4与x轴相交于点A和点B,与y轴相交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C,动点P以每秒2个单位长度的速度从C点出发,沿C→D运动,同时,点Q以每秒1个单位长度的速度从点A出发,沿A→B运动,连接PQ、CB,设点P运动的时间为t秒.
-4a-4与x轴相交于点A和点B,与y轴相交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C,动点P以每秒2个单位长度的速度从C点出发,沿C→D运动,同时,点Q以每秒1个单位长度的速度从点A出发,沿A→B运动,连接PQ、CB,设点P运动的时间为t秒.
(1)求a的值;
(2)当四边形ODPQ为矩形时,求这个矩形的面积;
(3)当四边形PQBC的面积等于14时,求t的值.
(4)当t为何值时,△PBQ是等腰三角形?


(2)由(1)可得抛物线的解析式为
y=x![]() -6x+8
-6x+8
当y=0时,x![]() -6x+8=0
-6x+8=0
解得:x![]() =2,x
=2,x![]() =4
=4
∴A点坐标为(2,0),B点坐标为(4,0)
当y=8时,
x=0或x=6
∴D点的![]() 坐标为(0,8),C点坐标为(6,8)
坐标为(0,8),C点坐标为(6,8)
DP=6-2t,OQ=2+t
当四边形OQPD为矩形时,DP=OQ
2+t=6-2t,t=![]() ,OQ=2+
,OQ=2+![]() =
=![]()
S=8×![]() =
=![]()
即矩形OQ![]() PD的面积为
PD的面积为![]()
(3)四边形PQBC的面积为![]() ,当此四边形的面积为14时,
,当此四边形的面积为14时,
![]() (2-t+2t)×8=14
(2-t+2t)×8=14
解得t=![]() (秒)
(秒)
当t=![]() 时,四边形PQBC的面积为14
时,四边形PQBC的面积为14
(4)t=![]() 时,PBQ是等腰三角形.
时,PBQ是等腰三角形.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 -ax+a
-ax+a
 -ax+a
-ax+a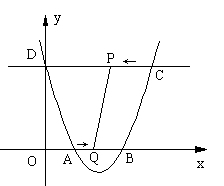
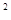 -ax+a
-ax+a