题目内容
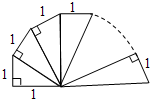
如图，以1为直角边长作直角三角形，以它的斜边长和1为直角边作第二个直角三角形，再以它的斜边和1为直角边作第三个直角三角形，则第三个直角三角形的斜边长为
2
2
．以此类推，所得第n个直角三角形的斜边长为| n+1 |
| n+1 |
分析：运用勾股定理求出各三角形的斜边，根据规律可得出第n个直角三角形的斜边长．
解答：解：第一个直角三角形的斜边=
=
；
第二个直角三角形的斜边=
=
；
第三个直角三角形的斜边=
=
=2；
第四个直角三角形的斜边=
=
；
…
第n个直角三角形的斜边=
；
故答案为：2、
．
| 1+1 |
| 2 |
第二个直角三角形的斜边=
| 2+1 |
| 3 |
第三个直角三角形的斜边=
| 3+1 |
| 4 |
第四个直角三角形的斜边=
| 4+1 |
| 5 |
…
第n个直角三角形的斜边=
| n+1 |
故答案为：2、
| n+1 |
点评：本题考查了勾股定理，解答本题的关键是运用勾股定理求出斜边，另外要求有一定的归纳总结能力．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
如图，以△ABC的直角边AB为直径的半圆O与斜边AC交于点D，E是BC边的中点，连接DE．
如图，以1为直角边长作直角三角形，以它的斜边长和1为直角边作第二个直角三角形，再以它的
