جâؤ؟ؤعبف
،¾جâؤ؟،؟خھءث¹ل³¹،°¼ُ¸؛شِذ§،±¾«ةٌ£¬صئخص¾إؤ꼶600أûر§ةْأ؟جىµؤ×شض÷ر§د°اé؟ِ£¬ؤ³ذ£ثو»ْ³é²éءث¾إؤ꼶µؤ²؟·ضر§ةْ£¬²¢µ÷²éثûأاأ؟جى×شض÷ر§د°µؤت±¼ن£®¸ù¾فµ÷²é½ل¹û£¬ضئ×÷ءثء½·ù²»حêصûµؤح³¼ئح¼بçح¼£¬اë¸ù¾فح³¼ئح¼ضذµؤذإد¢»ط´ًدآءذختجâ£؛
£¨1£©´ث´خ³éرùµ÷²éضذ£¬¹²µ÷²éءث¶àةظأûر§ةْ£؟
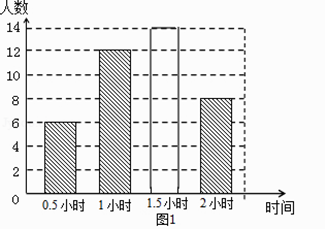
£¨2£©½«ح¼1²¹³نحêصû£» 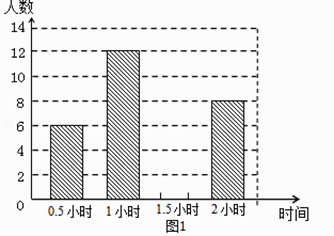
£¨3£©اَ³ِح¼2ضذش²ذؤ½ا¦ءµؤ¶بت£» 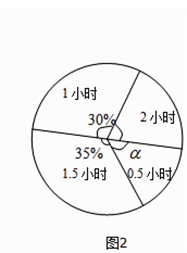
£¨4£©اë¹ہثم¸أذ£¾إؤ꼶ر§ةْ×شض÷ر§د°ت±¼ن²»ةظسع1.5ذ،ت±µؤسذ¶àةظبث£؟
،¾´ً°¸،؟
£¨1£©½â£؛12،آ30%=40بث£¬
´ً£؛¹²µ÷²éءث40أûر§ةْ£»
£¨2£©½â£؛×شض÷ر§د°ت±¼نµبسع1.5ذ،ت±µؤسذ40،ء35%=14بث£»
بçح¼ثùت¾£¬
£¨3£©½â£؛ش²ذؤ½ا¦ءµؤ¶بتتا360،م،ء ![]() =54،م£»
=54،م£»
£¨4£©½â£؛¸أذ£¾إؤ꼶ر§ةْ×شض÷ر§د°ت±¼ن²»ةظسع1.5ذ،ت±µؤسذ¶àةظبث600،ء ![]() =330بث£®
=330بث£®
،¾½âخِ،؟£¨1.£©¸ù¾ف1ذ،ت±µؤبثت؛حثùص¼µؤ°ظ·ض±ب£¬¼´؟ةاَ³ِ×ـبثت£» £¨2.£©سأ1.5ذ،ت±µؤبثتثùص¼µؤ°ظ·ض±ب³ثزش³é²éµؤبثت¼´؟ةاَ³ِ1.5ذ،ت±µؤبثت£¬´س¶ّ²¹ب«ح³¼ئح¼£»
£¨3.£©سأ0.5ذ،ت±µؤبثت³زش³é²éµؤبثت£¬شظ³ثزش360¶ب£¬¼´؟ةاَ³ِش²ذؤ½ا¦ءµؤ¶بت£»
£¨4.£©سأ×ـبثت³ثزش¸أذ£¾إؤ꼶ر§ةْ×شض÷ر§د°ت±¼ن²»ةظسع1.5ذ،ت±ثùص¼µؤ°ظ·ض±ب£¬¼´؟ةاَ³ِ¸أذ£¾إؤ꼶ر§ةْ×شض÷ر§د°ت±¼ن²»ةظسع1.5ذ،ت±µؤبثت£®

 شؤ¶ء؟ى³µدµءذ´ً°¸
شؤ¶ء؟ى³µدµءذ´ً°¸،¾جâؤ؟،؟°ث(2)°à×éض¯ءثز»´خ¾µنثذ¶ء±ببü£¬¼×،¢ززء½¶س¸÷10بثµؤ±ببü³ة¼¨بçدآ±ي(10·ضضئ)£؛
¼× | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
زز | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)¼×¶س³ة¼¨µؤضذخ»تتا ·ض£¬زز¶س³ة¼¨µؤضعتتا ·ض£»
(2)¼ئثمزز¶سµؤئ½¾ù³ة¼¨؛ح·½²î£»
(3)زرضھ¼×¶س³ة¼¨µؤ·½²îتا1.4£¬شٍ³ة¼¨½دخھصûئëµؤتا ¶س£®