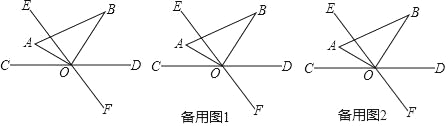
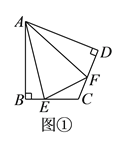题目内容
【题目】如图,![]() 中,
中,![]() ,
,![]() 、
、![]() 的平分线交于
的平分线交于![]() ,
,![]() 是
是![]() 延长线上一点,且
延长线上一点,且![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() .其中所有正确结论的序号有( ).
.其中所有正确结论的序号有( ).

A. ①② B. ①③ C. ②③ D. ①②③
【答案】D
【解析】根据三角形内角和等于180°求出∠ABC+∠ACB,再根据角平分线的定义求出∠EBC+∠ECB,然后求出∠BEC=120°,判断①正确;过点D作DF⊥AB于F,DG⊥AC的延长线于G,根据角平分线上的点到角的两边的距离相等可得DF=DG,再求出∠BDF=∠CDG,然后利用“角边角”证明△BDF和△CDG全等,根据全等三角形对应边相等可得BD=CD,再根据等边对等角求出∠DBC=30°,然后根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义求出∠DBE=∠DEB,根据等角对等边可得BD=DE,判断②正确,再求出B,C,E三点在以D为圆心,以BD为半径的圆上,根据同弧所对的圆周角等于圆心角的一半可得∠BDE=2∠BCE,判断③正确.
∵![]() ,
,
∴![]() ,
,
∵![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的平分线,
的平分线,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
故①正确.
如图,过点![]() 作
作![]() 于
于![]() ,
,![]() 的延长线于
的延长线于![]() ,
,
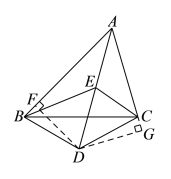
∵![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的平分线,
的平分线,
∴![]() 为
为![]() 的平分线,
的平分线,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ,
,
∵在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,
∴![]() ,
,![]() ,
,
根据三角形的外角性质,
![]() ,
,
∴![]() ,
,
∴![]() ,故②正确.
,故②正确.
∵![]() ,
,
∴![]() 、
、![]() 、
、![]() 三点在以
三点在以![]() 为圆心,以
为圆心,以![]() 为半径的圆上,
为半径的圆上,
∴![]() ,故③正确,
,故③正确,
综上所述,正确结论有①②③,
故选:![]() .
.

 阅读快车系列答案
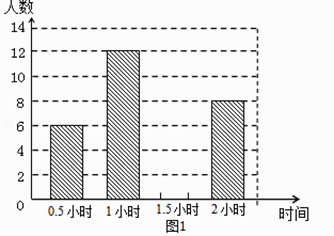
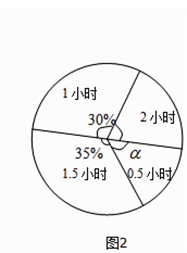
阅读快车系列答案【题目】网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,为了解市民对售后评价的关注情况,随机采访部分市民,对采访情况制作了如下统计图表:
关注情况 | 频数 | 频率 |
A.高度关注 | 50 | b |
B.一般关注 | 120 | 0.6 |
C.不关注 | a | 0.1 |
D.不知道 | 10 | 0.05 |
(1)根据上述统计图可得此次采访的人数为人,a= , b=;
(2)根据以上信息补全条形统计图; 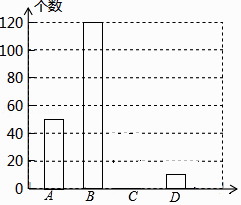
(3)根据上述采访结果,请估计在6400名市民中,高度关注售后评价的市民约有多少人?