题目内容
 如图所示,某水库大坝的横断面是梯形,坝顶宽CD=3m,坝高4m,背水坡的坡度是1:1.5,迎水坡的坡度是1:2.5,求坝底宽AB和坡角∠A.
如图所示,某水库大坝的横断面是梯形,坝顶宽CD=3m,坝高4m,背水坡的坡度是1:1.5,迎水坡的坡度是1:2.5,求坝底宽AB和坡角∠A.分析:过点D作DE⊥AB于点E,过点C作CF⊥AB于点F,在Rt△ADE中,根据背水坡的坡度是1:1.5,可得tanA的值,继而可得出坡角∠A;在Rt△ADE中求出AE,在Rt△CFB中求出BF,继而可得出AB.
解答:解:过点D作DE⊥AB于点E,过点C作CF⊥AB于点F,
 在Rt△ADE中,∵
在Rt△ADE中,∵
=
=tanA,
∴坡角∠A≈33.69°,AE=1.5DE=6,
在Rt△CFB中,∵
=
,
∴BF=2.5CF=2.5×4=10,
∴AB=AE+EF+BF=AE+CD+BF=19米.
答:坝底宽AB为19米,∠A约为33.69°.
 在Rt△ADE中,∵
在Rt△ADE中,∵| DE |
| AE |
| 1 |
| 1.5 |
∴坡角∠A≈33.69°,AE=1.5DE=6,
在Rt△CFB中,∵
| CF |
| BF |
| 1 |
| 2.5 |
∴BF=2.5CF=2.5×4=10,
∴AB=AE+EF+BF=AE+CD+BF=19米.
答:坝底宽AB为19米,∠A约为33.69°.
点评:本题考查了坡度、坡角的知识,解答本题的关键是构造直角三角形,要求同学们理解坡度的定义.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
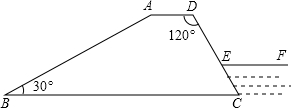
 如图所示,某水库大坝的横断面是梯形ABCD,坝顶宽CD=3m,斜坡AD=8m,斜坡BC的坡度i=1:3,B,C间的水平距离为12m,则斜坡AD的坡角∠A=
如图所示,某水库大坝的横断面是梯形ABCD,坝顶宽CD=3m,斜坡AD=8m,斜坡BC的坡度i=1:3,B,C间的水平距离为12m,则斜坡AD的坡角∠A= 如图所示,某水库大坝的横断面是梯形ABCD,坝顶宽CD=3m,斜坡AD=8m,斜坡BC的坡度i=1:3,B,C间的水平距离为12m,则斜坡AD的坡角∠A=________,坝底宽AB=________m.
如图所示,某水库大坝的横断面是梯形ABCD,坝顶宽CD=3m,斜坡AD=8m,斜坡BC的坡度i=1:3,B,C间的水平距离为12m,则斜坡AD的坡角∠A=________,坝底宽AB=________m.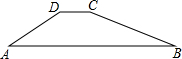 如图所示,某水库大坝的横断面是梯形,坝顶宽CD=3m,坝高4m,背水坡的坡度是1:1.5,迎水坡的坡度是1:2.5,求坝底宽AB和坡角∠A.
如图所示,某水库大坝的横断面是梯形,坝顶宽CD=3m,坝高4m,背水坡的坡度是1:1.5,迎水坡的坡度是1:2.5,求坝底宽AB和坡角∠A.