Question

如图，二次函数y＝x²＋bx－的图象与x轴交于点A(－3，0)和点B，以AB为边在x轴上方作正方形ABCD，点P是x轴上一动点，连接DP，过点P作DP的垂线与y轴交于点E．

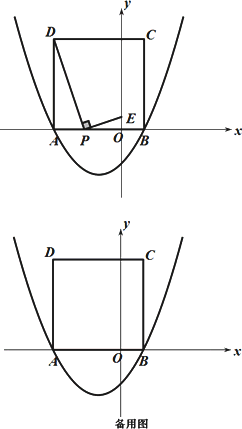
(1)请直接写出点D的坐标：________；

(2)当点P在线段AO(点P不与A，O重合)上运动至何处时，线段OE的长有最大值，求出这个最大值；

(3)是否存在这样的点P使△PED是等腰三角形？若存在，请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积；若不存在，请说明理由．

Answer 1

答案：
解析：

(1)(－3，4) 　　(2)设PA＝t，OE＝1， 　　由∠DAP＝∠POE＝∠DPE＝90°， 　　得△DAP∽△POE， 　　∴＝ 　　∴1＝－t2＋t＝－(t－)2＋ 　　∴当t＝时，1有最大值，即P为AO中点时，OE的最大值为．　4分 　　(3)存在 　　①当P在y轴左侧时，P点的坐标为(－4，0)　5分 　　由△PAD≌△PEO，得OE＝PA＝1，∴OP＝OA＋PA＝4， 　　∴AG＝AO＝， 　　∴重叠部分的面积＝×4×＝　7分 　　②当P在y轴右侧时，P点的坐标为(4，0)　8分 　　(仿照①的步骤，此时的重叠部分的面积为　10分