题目内容
【题目】如图,AD为△ABC的中线,BE为三角形ABD中线,
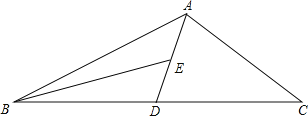
(1)∠ABE=15°,∠BAD=35°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为60,BD=5,则点E到BC边的距离为多少?
【答案】(1)50°(2)见解析;(3)6
【解析】
试题分析:(1)利用三角形的外角等于与它不相邻的两个内角之和即可求∠BED的度数;
(2)△BED是钝角三角形,所以BD边上的高在BD的延长线上;
(3)先根据三角形的中线把三角形分成面积相等的两个小三角形,结合题意可求得△BED的面积,再直接求点E到BC边的距离即可.
解:(1)∵∠BED是△ABE的一个外角,
∴∠BED=∠ABE+∠BAD=15°+35°=50°.
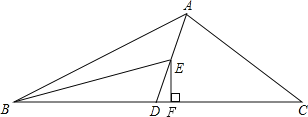
(2)如图所示,EF即是△BED中BD边上的高.
(3)∵AD为△ABC的中线,BE为三角形ABD中线,
∴S△BED=![]() S△ABC=
S△ABC=![]() ×60=15;
×60=15;
∵BD=5,
∴EF=2S△BED÷BD=2×15÷5=6,
即点E到BC边的距离为6.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目