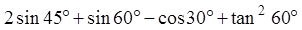题目内容
一条船上午8点在A处望见西南方向有一座灯塔B(如图),此时测得船和灯塔相距60海里,船以每小时30海里的速度向南偏西24º的方向航行到C处,这时望见灯塔在船的正北方向(参考数据:sin24º≈0.4,cos24º≈0.9)
小题1:求几点钟船到达C处
小题2:求船到达C处时与灯塔之间的距离.
小题1:求几点钟船到达C处
小题2:求船到达C处时与灯塔之间的距离.

小题1:AC= 150 150÷30="5" 小时
小题2:BC=150×cos24º-60=75海里
(1)要求几点到达C处,需要先求出AC的距离,根据时间=距离除以速度,从而求出解.
(2)船和灯塔的距离就是BC的长,作出CB的延长线交AD于E,根据直角三角形的角,用三角函数可求出CE的长,减去BE就是BC的长
(2)船和灯塔的距离就是BC的长,作出CB的延长线交AD于E,根据直角三角形的角,用三角函数可求出CE的长,减去BE就是BC的长

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 米
米 米
米
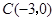 ,点
,点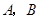 分别在
分别在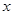 轴,
轴,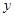 轴的正半轴上,且满足
轴的正半轴上,且满足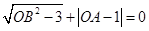 .
.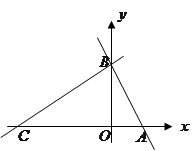
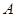 ,点
,点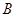 的坐标
的坐标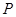 从
从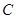 点出发,以每秒1个单位的速度沿线段
点出发,以每秒1个单位的速度沿线段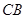 运动,连结
运动,连结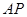 .设
.设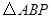 的面积为
的面积为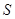 ,点
,点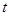 秒,求
秒,求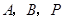 为顶点的三角形与
为顶点的三角形与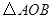 相似?若存在,请直接写出点
相似?若存在,请直接写出点 ,并沿东北方向
,并沿东北方向 移动,已知台风移动的速度为
移动,已知台风移动的速度为 千米/时,受影响区域的半径为
千米/时,受影响区域的半径为 千米,
千米, 市位于点
市位于点 方向上,与
方向上,与 千米.
千米.