Question

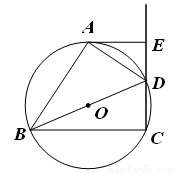
（本小题8分）如图，四边形ABCD内接于⊙O，BD是⊙O的直径，

AE⊥CD于点E，DA平分∠BDE．

（Ⅰ）求证：AE是⊙O的切线；

（Ⅱ）若∠DBC=30°，DE=1 cm，求BD的长．

 

Answer 1

【答案】

（Ⅰ）证明：连结OA

∵AD平分∠BDE

∴∠ADE＝∠ADO  ……………1分

∵OA=OD

∴∠OAD＝∠ADO ……………2分

∴∠ADE＝∠OAD             

∴OA∥CE           ……………3分

∵AE⊥CD

∴AE⊥OA            ……………4分       

∴AE是⊙O的切线            …………………………5分

（Ⅱ）∵BD是⊙O的直径

∴∠BCD＝90°                 

∵∠DBC=30°

∴∠BDE＝120°…………………………6分

∵AD平分∠BDE

∴∠ADE＝∠ADO=60°

∵OA=OD

∴△OAD是等边三角形          …………………………7分 

∴AD=OD=BD        

在Rt△AED中，DE=1，∠ADE=60°

∴AD= = 2                     

∴BD=4       …………………………8分                

【解析】略