题目内容

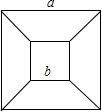精英家教网如图：大正方形的边长为a，小正方形的边长为b，利用此图证明平方差公式．
分析：由大正方形的面积-小正方形的面积=四个等腰梯形的面积，进而证得平方差公式．
解答：解：根据题意大正方形的面积-小正方形的面积=a2-b2，
四个等腰梯形的面积=
1
2
（a+b）（
1
2
a-
1
2
b）×4=（a+b）（a-b），
故a2-b2=（a+b）（a-b）．
点评：本题主要考查平方差公式的几何背景，不是很难．
练习册系列答案
相关题目
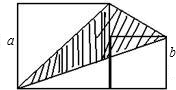精英家教网如图，大正方形的边长为a，小正方形的边长为b，用代数式表示图中阴影部分的面积，并求当a=8，b=6时代数式的值是多少？
精英家教网如图，大正方形的边长为a，小正方形的边长为2，求阴影部分的面积．
如图，大正方形的边长为
15
+
5
，小正方形的边长为
15
-
5
，求图中的阴影部分的面积．
一天，小明和小玲玩纸片拼图游戏，发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式．比如图②可以解释为：（a+2b）（a+b）=a2+3ab+2b2．
（1）图③可以解释为等式：
（a+2b）（2a+b）=2a2+5ab+2b2
（a+2b）（2a+b）=2a2+5ab+2b2

（2）要拼出一个长为a+3b，宽为2a+b的长方形，需要如图所示的
2
2
块，
7
7
块，
3
3
块．
（3）如图④，大正方形的边长为m，小正方形的边长为n，若用x、y表示四个矩形的两边长（x＞y），观察图案，指出以下关系式：
（1）xy=
m2-n2
4
（2）x+y=m（3）x2-y2=m•n（4）x2+y2=
m2+n2
2

其中正确的有
B
B

A．1个   B．2个    C．3个   D．4个．
如图，大正方形的边长是5厘米，小正方形的边长是4厘米，四边形AHFD（阴影部分）的面积是
12.5
12.5
平方厘米．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网