题目内容
抛物线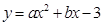 交
交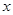 轴于
轴于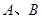 两点,交
两点,交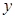 轴于点
轴于点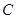 ,已知抛物线的对称轴为直线
,已知抛物线的对称轴为直线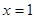 ,
,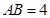 .
.
1.(1)求二次函数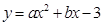 的解析式;
的解析式;
2.(2)在抛物线对称轴上是否存在一点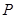 ,使点
,使点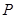 到
到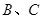 两点距离之差最大?若存在,求出
两点距离之差最大?若存在,求出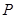 点坐标;若不存在,请说明理由;
点坐标;若不存在,请说明理由;
3.(3)平行于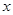 轴的一条直线交抛物线于
轴的一条直线交抛物线于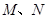 两点,若以
两点,若以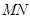 为直径的圆恰好与
为直径的圆恰好与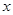 轴相切,求此圆的半径.
轴相切,求此圆的半径.
【答案】
1.(1)设抛物线的解析式为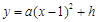 ,
,
∵点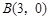 、
、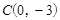 在抛物线上,
在抛物线上,
∴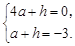 解得
解得
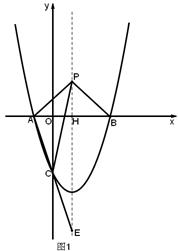
∴抛物线的解析式为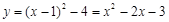 . ……………2分
. ……………2分
2. (2)
(2)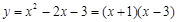 ,
,
∴A(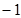 ,0),B(3,0).
,0),B(3,0).
∴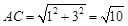 .
.
∴PA=PB,
∴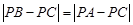 .
………..3分
.
………..3分
如图1,在△PAC中,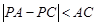 ,
,
当P在AC的延长线上时,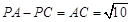 .
.
设直线AC的解析式为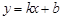 ,
,
∴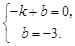
解得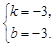
∴直线AC的解析式为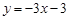 .
.
当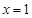 时,
时,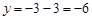 .
.
∴当点P的坐标为(1,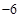 )时,
)时,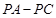 的最大值为
的最大值为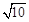 .…………….5分
.…………….5分
3.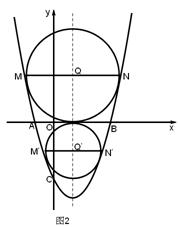 (3)如图2,当以MN为直径的圆与
(3)如图2,当以MN为直径的圆与 轴相切时,
轴相切时,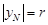 .
.
∵点N的横坐标为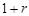 ,
,
∴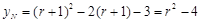 .
.
∴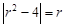 .
.
解得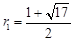 ,
,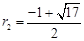 . ……………..7分
. ……………..7分
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(本题满分12分)在平面直角坐标系中,抛物线交 轴于
轴于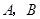 两点,交
两点,交 轴于点
轴于点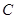 ,已知抛物线的对称轴为
,已知抛物线的对称轴为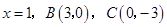 .
.
【小题1】⑴求这个抛物线的解析式;
【小题2】⑵在抛物线的对称轴上是否存在一点 ,使点
,使点 到A、C两点间的距离之和最大.若存在,求出点
到A、C两点间的距离之和最大.若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【小题3】(3)如果在 轴上方平行于
轴上方平行于 轴的一条直线交抛物线于
轴的一条直线交抛物线于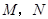 两点,以
两点,以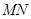 为直径作圆恰好与
为直径作圆恰好与 轴相切,求此圆的直径.
轴相切,求此圆的直径.
 轴于
轴于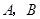 两点,交
两点,交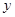 轴于点
轴于点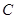 ,已知抛物线的对称轴为
,已知抛物线的对称轴为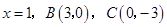 .
. |
【小题1】⑴求这个抛物线的解析式;
【小题2】⑵在抛物线的对称轴上是否存在一点
 ,使点
,使点 到A、C两点间的距离之和最大.若存在,求出点
到A、C两点间的距离之和最大.若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.【小题3】(3)如果在
 轴上方平行于
轴上方平行于 轴的一条直线交抛物线于
轴的一条直线交抛物线于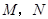 两点,以
两点,以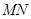 为直径作圆恰好与
为直径作圆恰好与 轴相切,求此圆的直径.
轴相切,求此圆的直径. 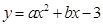 交
交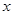 轴于
轴于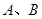 两点,交
两点,交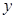 轴于点
轴于点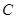 ,已知抛物线的对称轴为直线
,已知抛物线的对称轴为直线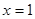 ,
,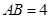 .
.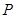 ,使点
,使点 两点距离之差最大?若存在,求出
两点距离之差最大?若存在,求出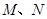 两点,若以
两点,若以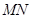 为直径的圆恰好与
为直径的圆恰好与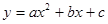 交
交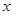 轴于
轴于 两点,交
两点,交 轴于点
轴于点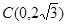 .
.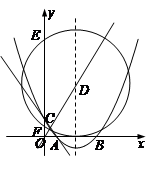
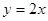 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交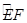 的长;
的长;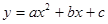 交
交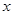 轴于
轴于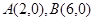 两点,交
两点,交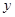 轴于点
轴于点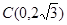 .
.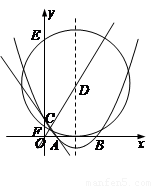
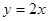 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交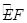 的长;
的长;