题目内容
 如图,把矩形OABC放在直角坐标系中,OC在x轴上,OA在y轴上,且OC=2,OA=4,把矩形OABC绕着原点顺时针旋转90°得到矩形ODEF,则E的坐标为( )
如图,把矩形OABC放在直角坐标系中,OC在x轴上,OA在y轴上,且OC=2,OA=4,把矩形OABC绕着原点顺时针旋转90°得到矩形ODEF,则E的坐标为( )分析:根据旋转变换只改变图形的位置不改变图形的形状与大小可得OD=OA,OF=OC,再根据点E在第一象限写出点E的坐标即可.
解答:解:∵矩形OABC绕着原点顺时针旋转90°得到矩形ODEF,
∴OD=OA=4,OF=OC=2,
又∵点E在第一象限,
∴点E的坐标为(4,2).
故选C.
∴OD=OA=4,OF=OC=2,
又∵点E在第一象限,
∴点E的坐标为(4,2).
故选C.
点评:本题考查了坐标与图形变化-旋转,熟记旋转变换只改变图形的位置不改变图形的形状与大小是解题的关键.

练习册系列答案
相关题目
 到折痕EF,连接OE、BF.
到折痕EF,连接OE、BF. 到折痕EF.
到折痕EF. 21、如图,把矩形OABC放在直角坐标系中,OC在x轴上,OA在y轴上,且OC=2,OA=4,把矩形OABC绕着原点顺时针旋转90°得到矩形OA′B′C′,则点B′的坐标为( )
21、如图,把矩形OABC放在直角坐标系中,OC在x轴上,OA在y轴上,且OC=2,OA=4,把矩形OABC绕着原点顺时针旋转90°得到矩形OA′B′C′,则点B′的坐标为( )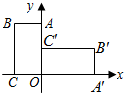 17、如图,把矩形OABC放在直角坐标系中,OC在x轴上,OA在y轴上,且OC=1,OA=2,把矩形OABC绕着原点顺时针旋转90°得到矩形OA'B'C',则点B'的坐标为
17、如图,把矩形OABC放在直角坐标系中,OC在x轴上,OA在y轴上,且OC=1,OA=2,把矩形OABC绕着原点顺时针旋转90°得到矩形OA'B'C',则点B'的坐标为