题目内容
 (2012•天津)如图,△ABC是⊙O的内接三角形,AB为⊙O的直径,点D为⊙O上一点,若∠CAB=55°,则∠ADC的大小为
(2012•天津)如图,△ABC是⊙O的内接三角形,AB为⊙O的直径,点D为⊙O上一点,若∠CAB=55°,则∠ADC的大小为35
35
(度).分析:由AB为⊙O的直径,根据直径所对的圆周角是直角,∠ACB=90°,又由直角三角形的两锐角互余,即可求得∠B的度数,然后根据在同圆或等圆中,同弧或等弧所对的圆周角相等,即可求得答案.
解答:解:∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠CAB=55°,
∴∠B=90°-∠CAB=35°,
∴∠ADC=∠B=35°.
故答案为:35°.
∴∠ACB=90°,
∵∠CAB=55°,
∴∠B=90°-∠CAB=35°,
∴∠ADC=∠B=35°.
故答案为:35°.
点评:此题考查了圆周角定理与直角三角形的性质.此题难度不大,注意直径所对的圆周角是直角与在同圆或等圆中,同弧或等弧所对的圆周角相等定理的应用,注意数形结合思想的应用.

练习册系列答案
相关题目
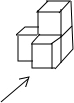 (2012•天津)如图是一个由4个相同的正方体组成的立体图形,它的三视图是( )
(2012•天津)如图是一个由4个相同的正方体组成的立体图形,它的三视图是( )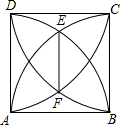 (2012•天津)如图,已知正方形ABCD的边长为1,以顶点A、B为圆心,1为半径的两弧交于点E,以顶点C、D为圆心,1为半径的两弧交于点F,则EF的长为
(2012•天津)如图,已知正方形ABCD的边长为1,以顶点A、B为圆心,1为半径的两弧交于点E,以顶点C、D为圆心,1为半径的两弧交于点F,则EF的长为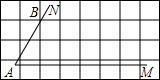 (2012•天津)“三等分任意角”是数学史上一个著名问题.已知一个角∠MAN,设∠α=
(2012•天津)“三等分任意角”是数学史上一个著名问题.已知一个角∠MAN,设∠α=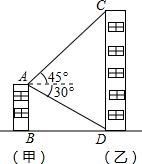 (2012•天津)如图,甲楼AB的高度为123m,自甲楼楼顶A处,测得乙楼顶端C处的仰角为45°,测得乙楼底部D处的俯角为30°,求乙楼CD的高度(结果精确到0.1m,
(2012•天津)如图,甲楼AB的高度为123m,自甲楼楼顶A处,测得乙楼顶端C处的仰角为45°,测得乙楼底部D处的俯角为30°,求乙楼CD的高度(结果精确到0.1m,