题目内容
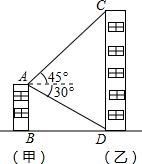（2012•天津）如图，甲楼AB的高度为123m，自甲楼楼顶A处，测得乙楼顶端C处的仰角为45°，测得乙楼底部D处的俯角为30°，求乙楼CD的高度（结果精确到0.1m，| 3 |
分析：首先分析图形，根据题意构造直角三角形．本题涉及多个直角三角形，应利用其公共边构造关系式求解．
解答：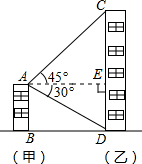
解：如图，过点A作AE⊥CD于点E，
根据题意，∠CAE=45°，∠DAE=30°．
∵AB⊥BD，CD⊥BD，
∴四边形ABDE为矩形．
∴DE=AB=123．
在Rt△ADE中，tan∠DAE=
，
∴AE=
=
=
=123
．
在Rt△ACE中，由∠CAE=45°，
得CE=AE=123
．
∴CD=CE+DE=123(
+1)≈335.8．
答：乙楼CD的高度约为335.8m．
解：如图，过点A作AE⊥CD于点E，根据题意，∠CAE=45°，∠DAE=30°．
∵AB⊥BD，CD⊥BD，
∴四边形ABDE为矩形．
∴DE=AB=123．
在Rt△ADE中，tan∠DAE=
| DE |
| AE |
∴AE=
| DE |
| tan∠DAE |
| 123 |
| tan30° |
| 123 | ||||
|
| 3 |
在Rt△ACE中，由∠CAE=45°，
得CE=AE=123
| 3 |
∴CD=CE+DE=123(
| 3 |
答：乙楼CD的高度约为335.8m．
点评：考查了解直角三角形的应用-仰角俯角问题，本题要求学生借助俯角构造直角三角形，并结合图形利用三角函数解直角三角形．
练习册系列答案
导学全程练创优训练系列答案
相关题目
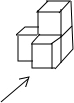（2012•天津）如图是一个由4个相同的正方体组成的立体图形，它的三视图是（ ）
（2012•天津）如图，△ABC是⊙O的内接三角形，AB为⊙O的直径，点D为⊙O上一点，若∠CAB=55°，则∠ADC的大小为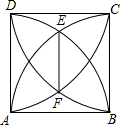
（2012•天津）如图，已知正方形ABCD的边长为1，以顶点A、B为圆心，1为半径的两弧交于点E，以顶点C、D为圆心，1为半径的两弧交于点F，则EF的长为
（2012•天津）“三等分任意角”是数学史上一个著名问题．已知一个角∠MAN，设∠α=