题目内容
为了开展阳光体育运动,坚持让中小学生“每天锻炼一小时”,某市教师培训与资源中心体育组搞了一个随机调查,调查内容是:“每天锻炼是否超过1小时及锻炼未超过1小时的原因”,他们随机调查了720名学生,所得的数据制成了如下的扇形统计图和频数分布直方图.

根据图示,请你回答以下问题:
(1)在随机调查的720名学生中,锻炼未超过1小时的学生有
(2)若2010年该市中小学生总人数约41.2万人,按此调查,可以估计2010年全市中小学生每天锻炼超过1小时约有
(3)假设2010至2012年该市中小学生总人数不变,保持41.2万人,如果计划2012年该市中小学生每天锻炼超过1小时的人数提高到26.368万人,求2010年至2012年每天锻炼超过1小时的人数的年平均增长率是多少?

根据图示,请你回答以下问题:
(1)在随机调查的720名学生中,锻炼未超过1小时的学生有
540
540
名,其中锻炼未超过1小时的原因是“没时间”的学生有400
400
名,并根据结果补全频数分布直方图;(2)若2010年该市中小学生总人数约41.2万人,按此调查,可以估计2010年全市中小学生每天锻炼超过1小时约有
1.03×105
1.03×105
人(请用科学记数法表示);(3)假设2010至2012年该市中小学生总人数不变,保持41.2万人,如果计划2012年该市中小学生每天锻炼超过1小时的人数提高到26.368万人,求2010年至2012年每天锻炼超过1小时的人数的年平均增长率是多少?
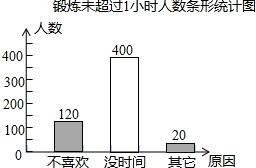
分析:(1)先求出2009年全市中小学生每天锻炼未超过1小时共有540人,再求没时间”的人数是540-120-20=400;
(2)用样本估计总体即可;
(3)设降低的百分率是x,则降低n次以后的人数是24(1-x)n,列出一元二次方程的解题即可.
(2)用样本估计总体即可;
(3)设降低的百分率是x,则降低n次以后的人数是24(1-x)n,列出一元二次方程的解题即可.
解答:解:(1)锻炼超过1小时的有720×
=540(人),
没时间的有540-120-20=400(人);
频数分布图:
(2)412000×
=1.03×105…(5分)
(3)解:设年平均增长率为x,由题意得10.3×(1+x)2=26.368…(7分)
解得 x1=0.6 x2=-2.6(不合题意,舍去)
即年平均增长率为60%
答:年平均增长率为60%.
| 270 |
| 360 |
没时间的有540-120-20=400(人);
频数分布图:

(2)412000×
| 360-270 |
| 360 |
(3)解:设年平均增长率为x,由题意得10.3×(1+x)2=26.368…(7分)
解得 x1=0.6 x2=-2.6(不合题意,舍去)
即年平均增长率为60%
答:年平均增长率为60%.
点评:此题主要考查了一元二次方程的应用,扇形统计图与条形统计图,常见错误:有些同学忘记画直方图.画频数分布图不规范,没用直尺和三角板等作图工具来完成,画图的随意性太大.题(3):对解一元二次方程的失根、验根没有掌握透彻.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 到3.84万人,求2006年至2008年锻炼未超过1小时人数的年平均降低的百分率是多少?
到3.84万人,求2006年至2008年锻炼未超过1小时人数的年平均降低的百分率是多少?
