Question

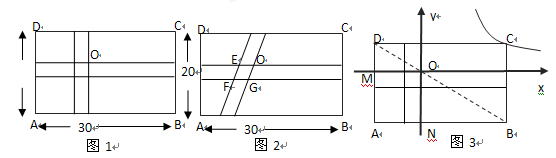
学生生物小组有一块长30m,宽20m的矩形ABCD试验田，为了管理方便，准备沿平行于两边的方向纵、横各开辟一条等宽的小道如图1,要使种植面积为504m².

问题探究：

（1）如图1，小道的宽应设计为多少m?

（2）若设计者将图1中纵向小道变成如图2所示的一条与横向小道等宽的小道，请你说明两小道重叠部分四边形EFGO是什么特殊的四边形？此时种植面积       （填变化或不变）

（3）若设计者将图1中小道边交叉点O落在矩形ABCD的对角线BD上，并建立如图3所示的直角坐标系,且满足OM=ON，请你求出点A的坐标及过点C的反比例函数的关系式.

 

Answer 1

【答案】

（1）2米，（2）菱形，变化，（3）A（-12，-12），

【解析】（1）设小道宽为X，则种植面积504=（30-x）(20-x)

化简得X²-50X+96=0   (X-2)( X-48)=0解得X=2或X=48（＞20舍去）

所以小道的宽为2米              -----4分

（2）过O作,分别交FE、FG于M、N两点

由题意知，(两直线平行，同位角相等)

所以△OME≌△ONG

所以OE=OG

四边形EFGO是菱形       -----3分

此时种植面积=FG ON,由勾股定理知

原来的种植面积=ONON

所以此时种植面积比原来的种植面积大，

故添变化   -----1分

（3）设OM长为X,由题意得，D(x,20-x),B(30-x,x)

设过点D、B的正比例函数为y=kx,

把D、B代入函数y=kx，求得x=12

即A（-12，-12）,

所以C(18,8)

代入y=k/x,得，