题目内容
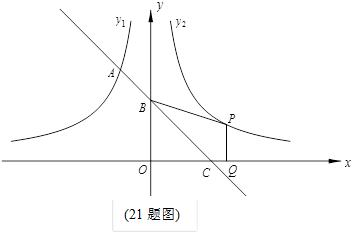
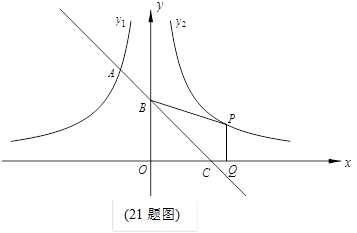
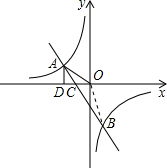
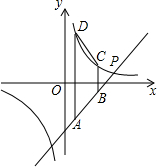
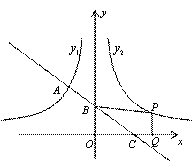
如图,一次函数的图象与反比例函数的图象交于A,B两点,与x轴交于点C,过A作AD⊥x轴于D,若OA= ,AD=
,AD= OD,点B
OD,点B 的横坐标为
的横坐标为
(1)求一次函数的解析式及△AOB的面积.
(2)已知反比例函数y1和一次函数y2,结合图象直接写出:当y1>y2时,x的取值范围.
(3)在坐标轴上是否存在点P使△OAP为等腰三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.
解:(1)如图,连接OB,在Rt△AOD中,OA= ,AD=
,AD= OD,且OD2+AD2=OA2,
OD,且OD2+AD2=OA2,
代入解得AD=1,OD=2,故A(-2,1),设B点纵坐标为h,已知B点横坐标为 ,
,
则(-2)×1= h,
h,
解得h=-4,
故B( ,-4),
,-4),
设直线AB解析式为y=kx+b,则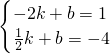 ,
,
 得
得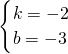 ,
,
直线AB解析式为y=-2x-3,由此可得C(- ,0),
,0),
所以,S△AOB=S△AOC+S△BOC= ×
× ×(1+4)=
×(1+4)=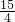 ;
;
(2)当y1>y2时,x的取值范围是:-2<x<0或x> ;
;
(3)存在点P使△OAP为等腰三角形,
此时,P点坐标为( ,0),(0,
,0),(0, ),(-4,0),(0,2),(-
),(-4,0),(0,2),(- ,0),(
,0),( ,0),(0,
,0),(0, ),(0,-
),(0,- ).
).
分析:(1)连接OB,在Rt△AOD中,由勾股定理求OD、AD,确定A点坐标,根据反比例函数图象上的点横坐标与纵坐标的积不变,求B点纵坐标,根据A、B两点坐标求直线AB的解析式,根据直线AB的解析式求OC的长,求△AOB的面积;
(2)根据A、B两点的横坐标,可求当y1>y2时,x的取值范围;
(3)①当AO为等腰三角形的底时,作线段OA的中垂线,与坐标轴相交,有两交点为所求P点;
②当OA为腰,点A为顶点时,以A为圆心,OA长为半径圆弧,与坐标轴相交,有两交点为所求P点;
当OA为腰,点O为顶点时,以O为圆心,OA长为半径圆弧,与坐标轴相交,有四个交点即为所求P点.
点评:本题考查了反比例函数的综合运用.关键是根据勾股定理求A点坐标,根据反比例函数图象上点的特点求B点坐标,确定直线AB的解析式,再结合图象的性质,等腰三角形的性质解题.
 ,AD=
,AD= OD,且OD2+AD2=OA2,
OD,且OD2+AD2=OA2,代入解得AD=1,OD=2,故A(-2,1),设B点纵坐标为h,已知B点横坐标为
 ,
,则(-2)×1=
 h,
h,解得h=-4,
故B(
 ,-4),
,-4),设直线AB解析式为y=kx+b,则
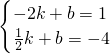 ,
, 得
得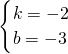 ,
,直线AB解析式为y=-2x-3,由此可得C(-
 ,0),
,0),所以,S△AOB=S△AOC+S△BOC=
 ×
× ×(1+4)=
×(1+4)=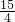 ;
;(2)当y1>y2时,x的取值范围是:-2<x<0或x>
 ;
;(3)存在点P使△OAP为等腰三角形,
此时,P点坐标为(
 ,0),(0,
,0),(0, ),(-4,0),(0,2),(-
),(-4,0),(0,2),(- ,0),(
,0),( ,0),(0,
,0),(0, ),(0,-
),(0,- ).
).分析:(1)连接OB,在Rt△AOD中,由勾股定理求OD、AD,确定A点坐标,根据反比例函数图象上的点横坐标与纵坐标的积不变,求B点纵坐标,根据A、B两点坐标求直线AB的解析式,根据直线AB的解析式求OC的长,求△AOB的面积;
(2)根据A、B两点的横坐标,可求当y1>y2时,x的取值范围;
(3)①当AO为等腰三角形的底时,作线段OA的中垂线,与坐标轴相交,有两交点为所求P点;
②当OA为腰,点A为顶点时,以A为圆心,OA长为半径圆弧,与坐标轴相交,有两交点为所求P点;
当OA为腰,点O为顶点时,以O为圆心,OA长为半径圆弧,与坐标轴相交,有四个交点即为所求P点.
点评:本题考查了反比例函数的综合运用.关键是根据勾股定理求A点坐标,根据反比例函数图象上点的特点求B点坐标,确定直线AB的解析式,再结合图象的性质,等腰三角形的性质解题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 如图,已知反比例函数y=
如图,已知反比例函数y=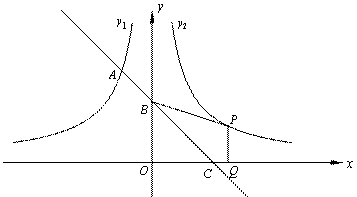
 解答:
解答: