Question

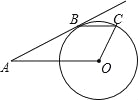
【题目】如图，AB切⊙O于点B，OA=5，tanA=，弦BC∥OA

（1）求AB的长

（2）求四边形AOCB的面积．

Answer 1

【答案】（1）10；（2）35

【解析】试题分析：（1）连接OB，由∠A的正切值可设OB=x，则AB=2x，再利用勾股定理计算即可；（2）过点O作OD⊥BC于点D，易证∠A=∠BOD，tan∠BOD=tan∠A=，进而可求出OD，BC的值，再利用梯形的面积公式计算即可．

试题解析：

（1）连接OB，

∵AB切⊙O于点B，

∴∠ABO=90°，

设OB=x，

在Rt△ABO中，tanA== ，设OB=x，则AB=2x，

∵OA= = x，

∴ x=5 ，

解得：x=5，

∴AB=10；

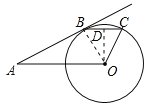
（2）过点O作OD⊥BC于点D，

∵BC∥OA，

∴∠AOB=∠DBO，

∵∠A+∠AOB=90°，∠BOD+∠AOB=90°，

∴∠A=∠BOD，

∴tan∠BOD=tan∠A=，

∴BD= ，OD=2 ，

∵OD⊥BC，

∴BC=2 ，

∴四边形AOCB的面积= （OA+BC）OD=35．