��Ŀ����
����Ŀ��ijУ���꼶ѧ����Ұ����Ϊ����һ��������A��B�ľ��룬�ס��ҡ�����λͬѧ�ֱ���Ƴ����¼��ַ����� 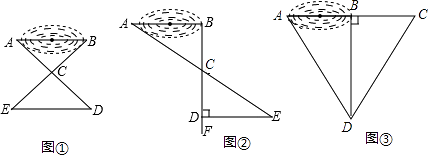
�ף���ͼ�٣�����ƽ��ȡһ����ֱ�ӵ���A��B�ĵ�C��������AC��BC�����ֱ��ӳ�AC��D��BC��E��ʹDC=AC��EC=BC�������DE�ij���ΪA��B�ľ��룮
�ң���ͼ�ڣ��ȹ���B��AB�Ĵ���BF������BF��ȡC��D���㣬ʹBC=CD�����Ź���D��BD�Ĵ���DE����AC���ӳ����ڵ�E������DE�ij���ΪA��B�ľ��룮
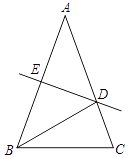
������ͼ�ۣ�����B��BD��AB�����ɵ�D�۲⣬��AB���ӳ�����ȡһ��C��ʹ��BDC=��BDA����ʱֻҪ���BC�ij���ΪA��B�ľ��룮
��1��������λͬѧ����Ƶķ��������е�����
��2������ѡ��һ���еķ�����˵˵�����е����ɣ�
���𰸡�
��1���ס��ҡ���
��2���⣺�𰸲�Ψһ��
ѡ�ף��ڡ�ABC�͡�DEC�� 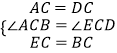 ��
��
���ABC�ա�DEC��SAS����
��AB=ED��
ѡ�ң���AB��BD��DE��BD��
���B=��CDE=90�㣬
�ڡ�ABC�͡�EDC�� 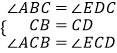 ��
��
���ABC�ա�EDC��ASA����
��AB=ED��
ѡ����
�ڡ�ABD�͡�CBD�� 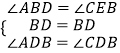 ��
��
���ABD�ա�CBD��ASA����
��AB=BC
���������⣺��1���ס��ҡ�����

��ϰ��ϵ�д�
 �Ͻ�ƽ��У����ϵ�д�
�Ͻ�ƽ��У����ϵ�д�
�����Ŀ