题目内容
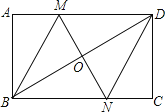
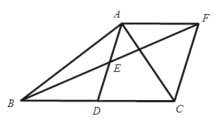
【题目】如图,在ABC 中, AD 是 BC 边上的中线,点 E 是 AD 的中点,过点 A 作AF // BC 交 BE 的延长线于 F ,连接CF .
(1)求证: AEF DEB ;
(2)若BAC 90,试判断四边形 ADCF 的形状,并证明你的结论;
(3)在(2)的情况下,如果 AC 2 ,点 M 在 AC 线段上移动,当 MB MD 有最小值时,求 AM 的长度(提示:以 D 点为原点, AD 为 y 正半轴, DC 为 x 正轴建立平面直角坐标系).
【答案】(1)证明见解析;(2)四边形ADCF是菱形;(3)![]() .
.
【解析】
(1)根据平行线的性质得到∠AFE=∠DBE,利用AAS定理证明△AEF≌△DEB;
(2)根据全等三角形的性质得到AF=DC,得到四边形ADCF是平行四边形,根据直角三角形的性质得到AD=DC,即可证明四边形ADCF是菱形;
(3)根据菱形的性质得到点D与点F关于直线AC对称,根据轴对称的性质作图即可得出点M,然后根据相似三角形的判定与性质即可得出AM与AC的关系,即可得出结论.
(1)∵AF∥BC,∴∠AFE=∠DBE.在△AEF和△DEB中,∵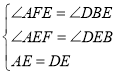 ,∴△AEF≌△DEB;
,∴△AEF≌△DEB;
(2)四边形ADCF是菱形,理由如下:
∵△AEF≌△DEB,∴AF=BD.
∵BD=DC,∴AF=DC.
又∵AF∥BC,∴四边形ADCF是平行四边形.
∵∠BAC=90°,AD是BC边上的中线,∴AD=DC,∴四边形ADCF是菱形;
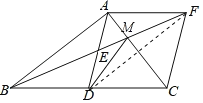
(3)连接BF交AC于M,则点M即为所求.
∵四边形ADCF是菱形,∴点D与点F关于直线AC对称,∴MD=MF,∴MB+MD=MB+MF=BF,即MB+MD有最小值.
∵AF=DC=BD,∴BC=2AF.
∵AF∥BC,∴△AMF∽△CMB,∴![]() ,∴
,∴![]() ,∴AM=
,∴AM=![]() AC.
AC.
∵AC=2,∴AM=![]() .
.

【题目】大学生自主创业,集资5万元开品牌专卖店,已知该品牌商品成本为每件a元,市场调查发现日销售量y(件)与销售价x(元/件)之间存在一次函数关系如表:
销售价x(元/件) | … | 110 | 115 | 120 | 125 | 130 | … |
销售量y(件) | … | 50 | 45 | 40 | 35 | 30 | … |
若该店某天的销售价定为110元/件,雇有3名员工,则当天正好收支平衡(其中支出=商品成本+员工工资+应支付其它费用):已知员工的工资为每人每天100元,每天还应支付其它费用为200元(不包括集资款).
(1)求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)该店现有2名员工,试求每件服装的销售价定为多少元时,该服装店每天的毛利润最大:(毛利润═销售收入一商品成本一员工工资一应支付其他费用)
(3)在(2)的条件下,若每天毛利润全部积累用于一次性还款,而集资款每天应按其万分之二的利率支付利息,则该店最少需要多少天(取整数)才能还清集资款?