题目内容
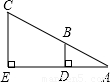
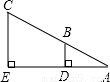
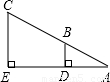
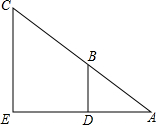 如图,小东设计两个直角,来测量河宽DE,他量得AD=2m,BD=3m,CE=9m,则河宽DE为
如图,小东设计两个直角,来测量河宽DE,他量得AD=2m,BD=3m,CE=9m,则河宽DE为分析:要求出DE,可以先求出AE,而AE可以利用△ADB∽△AEC,它们对应线段成比例去求.
解答:解:依题意得BD∥CE
∴△ADB∽△AEC.
∴
=
∴
=
∴AE=6
∴DE=AE-AD=6-2=4m.
∴△ADB∽△AEC.
∴
| AD |
| AE |
| BD |
| CE |
∴
| 2 |
| AE |
| 3 |
| 9 |
∴AE=6
∴DE=AE-AD=6-2=4m.
点评:本题只要是把实际问题抽象到相似三角形中,利用相似三角形的对应边成比例就可以.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
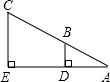 如图,小东设计两个直角,来测量河宽DE,他量得AD=2m,BD=3m,CE=9m,则河宽DE为( )
如图,小东设计两个直角,来测量河宽DE,他量得AD=2m,BD=3m,CE=9m,则河宽DE为( )| A、5m | B、4m | C、6m | D、8m |