题目内容
如图,四边形OABC为直角梯形,A(4,0)、B(3,4)、C(0,4),点M从O出发以每秒2个单位的速度向A运动,点N从B同时出发以每秒1个单位的速度向C运动,其中一个动点到达终点时,另一个动点也随之停止运动,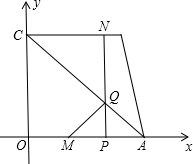 过点N作NP⊥x轴于点P,连接AC交NP于Q,连接MQ、设运动时间为t秒,
过点N作NP⊥x轴于点P,连接AC交NP于Q,连接MQ、设运动时间为t秒,(1)求AC所在直线的解析式;
(2)请用含t的代数式直接写出点Q的坐标;
(3)试写出△AQM的面积S与时间t的函数关系式,并求出其最大面积;
(4)是否存在点M,使△AQM为直角三角形?若存在,求出点M的坐标;若不存在,请说明理由.
分析:(1)设AC所在直线的解析式为:y=kx+b(k≠0),知道直线上两点可以求出k、b,
(2)点N从B同时出发以每秒1个单位的速度向C运动,且NP⊥x轴,又知OA=OC,可知NC=NQ,故能知道Q点坐标,
(3)由三角形面积公式直接写出含有t的二次函数关系式,求最值,
(4)分类讨论直角三角形的直角顶点,然后解出t,求得M坐标.
(2)点N从B同时出发以每秒1个单位的速度向C运动,且NP⊥x轴,又知OA=OC,可知NC=NQ,故能知道Q点坐标,
(3)由三角形面积公式直接写出含有t的二次函数关系式,求最值,
(4)分类讨论直角三角形的直角顶点,然后解出t,求得M坐标.
解答:解:(1)设AC所在直线的解析式为:y=kx+b(k≠0).
由
,
解得
.
∴AC所在直线的解析式为:y=-x+4.(3分)
(2)点Q(3-t,t+1).(5分)
(3)S△AQM=
(4-2t)(t+1)=-t2+t+2=-(t-
)2+
.(7分)
 当t=
当t=
时,S最大值=
.(8分)
(4)存在使△AQM为直角三角形的点M.(9分)
∵∠AOC=90°,OA=OC,
∴∠OAC=45°
即点A不可能为Rt△AQM的直角顶点.(9分)
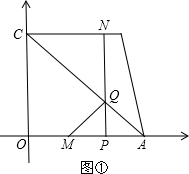
①当点Q为直角顶点时.(如图①)
∵∠MQA=90°,∠MAQ=45°,
∴MQ=QA
∵QP⊥AM∴AP=MP=PQ
 即
即
=t+1,
∴t=
则M(1,0).(10分)
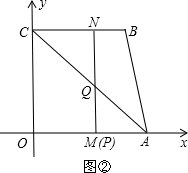
②当点M为直角顶点时.(如图②)
∵∠QMA=90°,∠MAQ=45°,
∴MQ=MA
即4-2t=t+1,
∴t=1,则M(2,0).(11分)
综上所述:点M的坐标为(1,0)或(2,0).(12分)
由
|
解得
|
∴AC所在直线的解析式为:y=-x+4.(3分)
(2)点Q(3-t,t+1).(5分)
(3)S△AQM=
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 4 |
 当t=
当t=| 1 |
| 2 |
| 9 |
| 4 |
(4)存在使△AQM为直角三角形的点M.(9分)
∵∠AOC=90°,OA=OC,
∴∠OAC=45°
即点A不可能为Rt△AQM的直角顶点.(9分)
①当点Q为直角顶点时.(如图①)
∵∠MQA=90°,∠MAQ=45°,
∴MQ=QA
∵QP⊥AM∴AP=MP=PQ
 即
即| 4-2t |
| 2 |
∴t=
| 1 |
| 2 |
②当点M为直角顶点时.(如图②)
∵∠QMA=90°,∠MAQ=45°,
∴MQ=MA
即4-2t=t+1,
∴t=1,则M(2,0).(11分)
综上所述:点M的坐标为(1,0)或(2,0).(12分)
点评:本题主要考查二次函数的最值等知识点,结合图形的面积,渗透分类讨论的思想,使问题综合性增强.

练习册系列答案
相关题目
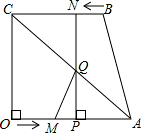 动.过点N作NP⊥OA于点P,连接AC交NP于Q,连接MQ.
动.过点N作NP⊥OA于点P,连接AC交NP于Q,连接MQ. 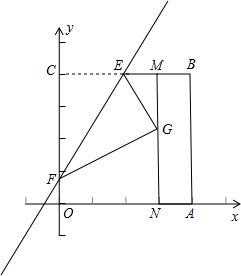 在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点.
在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点.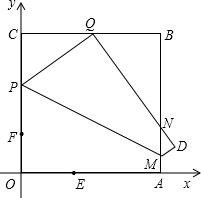
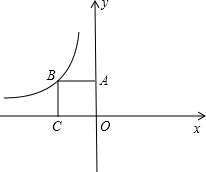 (2012•呼伦贝尔)如图,四边形OABC是边长为2的正方形,反比例函数
(2012•呼伦贝尔)如图,四边形OABC是边长为2的正方形,反比例函数 是( )
是( )