题目内容
【题目】如图，方格纸中每个小正方形的边长均为1，四边形ABCD的四个顶点都在小正方形的顶点上，点E在BC边上，且点E在小正方形的顶点上，连接AE．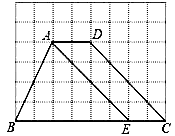
（1）在图中画出△AEF，使△AEF与△AEB关于直线AE对称，点F与点B是对称点，并求出BF的长；
（2）△AEF与四边形ABCD重叠部分的面积为 ．
【答案】
（1）解：如图1所示：
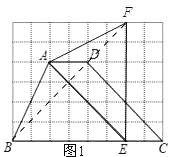
在Rt△BEF中，由勾股定理得：BF= 
（2）6
【解析】（1）根据轴对称的性质确定出点B关于AE的对称点F即可；
（2）如图2所示
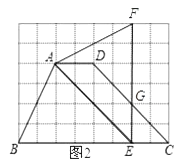
重叠部分的面积=SADEC-S△GEC
= 
×（2+2）×4- 
=8-2
=6．
（1）利用轴对称的性质确定出点B关于AE的对称点F即可；
（2）设DC与EF的交点为G，由四边形ADGE的面积=平行四边形ADCE的面积-△ECG的面积求解即可．
练习册系列答案
阅读快车系列答案
相关题目
