题目内容
【题目】如图,已知:△ABC中,AB=AC,BD和CE分别是∠ABC和∠ACB的角平分线,且相交于O点. ①试说明△OBC是等腰三角形;
②连接OA,试判断直线OA与线段BC的关系,并说明理由.
【答案】解:①∵在△ABC中,AB=AC, ∴∠ABC=∠BCA;
∵BD、CE分别平分∠ABC、∠BCA,
∴∠OBC=∠BCO;
∴OB=OC,
∴△OBC为等腰三角形.
②在△AOB与△AOC中.
∵ 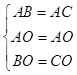 ,
,
∴△AOB≌△AOC(SSS);
∴∠BAO=∠CAO;
∴直线AO垂直平分BC.(等腰三角形顶角的平分线、底边上的高、底边上的中线互相重合)
【解析】①根据对边对等角得到∠ABC=∠ACB,再结合角平分线的定义得到∠OBC=∠OCB,从而证明OB=OC;②首先根据全等三角形的判定和性质得到OA平分∠BAC,再根据等腰三角形的三线合一的性质得到直线AO垂直平分BC.

练习册系列答案
相关题目