题目内容
观察规律填空
(1)从2开始,连续偶数相加和的情况如下:
2=1×2
2+4=2×3
2+4+6=3×4
2+4+6+8=4×5
计算:
①2+4+…+100= ;
②2+4+…+2n= .
(2)观察下列各式:
12+1=1×2
22+2=2×3
32+3=3×4
计算:
①202+20= ;
②n2+n= .
(1)从2开始,连续偶数相加和的情况如下:
2=1×2
2+4=2×3
2+4+6=3×4
2+4+6+8=4×5
计算:
①2+4+…+100= ;
②2+4+…+2n= .
(2)观察下列各式:
12+1=1×2
22+2=2×3
32+3=3×4
计算:
①202+20= ;
②n2+n= .
(1)①2550,②n(n+1);(2)①420,②n(n+1)
(1) 由从2开始,连续偶数相加和等于偶数的个数与它的个数加一的积.
2+4+…+100是50个偶数相加故等于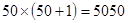 ;
;
同理2+4+…+2n是n个偶数相加故等于 .
.
(2)可以直接逆用乘法分配率,202+20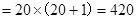 ,
,
n2+n
2+4+…+100是50个偶数相加故等于
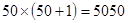 ;
;同理2+4+…+2n是n个偶数相加故等于
 .
.(2)可以直接逆用乘法分配率,202+20
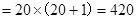 ,
,n2+n


练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
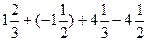 (2)
(2)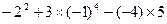
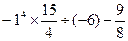 (4)用简便方法计算:
(4)用简便方法计算: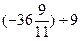
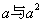 的大小.
的大小.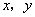 为实数,且
为实数,且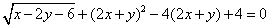 ,求
,求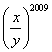 的值.
的值.




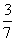 、
、 、
、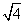 中,无理数是( ).
中,无理数是( ).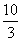
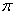
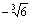 的绝对值是______。
的绝对值是______。