题目内容
 (2013•荆门)如图,在半径为1的⊙O中,∠AOB=45°,则sinC的值为( )
(2013•荆门)如图,在半径为1的⊙O中,∠AOB=45°,则sinC的值为( )分析:首先过点A作AD⊥OB于点D,由在Rt△AOD中,∠AOB=45°,可求得AD与OD的长,继而可得BD的长,然后由勾股定理求得AB的长,继而可求得sinC的值.
解答: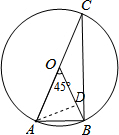 解:过点A作AD⊥OB于点D,
解:过点A作AD⊥OB于点D,
∵在Rt△AOD中,∠AOB=45°,
∴OD=AD=OA•cos45°=
×1=
,
∴BD=OB-OD=1-
,
∴AB=
=
,
∵AC是⊙O的直径,
∴∠ABC=90°,AC=2,
∴sinC=
.
故选B.
 解:过点A作AD⊥OB于点D,
解:过点A作AD⊥OB于点D,∵在Rt△AOD中,∠AOB=45°,
∴OD=AD=OA•cos45°=
| ||
| 2 |
| ||
| 2 |
∴BD=OB-OD=1-
| ||
| 2 |
∴AB=
| AD2+BD2 |
2-
|
∵AC是⊙O的直径,
∴∠ABC=90°,AC=2,
∴sinC=
| ||||
| 2 |
故选B.
点评:此题考查了圆周角定理、三角函数以及勾股定理.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
 (2013•荆门)如右图所示,已知等腰梯形ABCD,AD∥BC,若动直线l垂直于BC,且向右平移,设扫过的阴影部分的面积为S,BP为x,则S关于x的函数图象大致是( )
(2013•荆门)如右图所示,已知等腰梯形ABCD,AD∥BC,若动直线l垂直于BC,且向右平移,设扫过的阴影部分的面积为S,BP为x,则S关于x的函数图象大致是( ) (2013•荆门)如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过D点作AB的垂线交AC于点E,BC=6,sinA=
(2013•荆门)如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过D点作AB的垂线交AC于点E,BC=6,sinA=
