题目内容
下列命题中真命题是
- A.两个等腰三角形一定全等
- B.正多边形的每一个内角的度数随边数增多而减少
- C.菱形既是中心对称图形,又是轴对称图形
- D.两直线平行,同旁内角相等
C
分析:根据真命题和假命题的概念对四个选项逐一分析,即可解答.
A、根据等腰三角形的性质和三角形全等判定来判断,举出一个反例即可证明其为假命题;
B、根据内角和外角是互余关系,将内角的变化转化为外角的变化来解答;
C、根据菱形的定义和性质进行判断;
D、根据平行线的性质进行判断.
解答: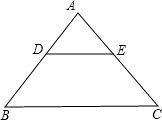 解:A、假命题,因为如图所示:AD=AE,AB=AC,但△ADE与△ABC不全等;
解:A、假命题,因为如图所示:AD=AE,AB=AC,但△ADE与△ABC不全等;
B、假命题,因为任何多边形的外角和均为360°,则其每个外角为α=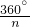 ,可见,当n增大时,α减小;
,可见,当n增大时,α减小;
C、真命题,因为菱形的对角线是其对称轴,两条对角线的交点是对称中心;
D、假命题,因为两直线平行,同旁内角互补.
故选C.
点评:本题考查的是全等三角形的判定定理、多边形的内角和定理、菱形的性质及平行线的性质,涉及面较广,但较为简单.
分析:根据真命题和假命题的概念对四个选项逐一分析,即可解答.
A、根据等腰三角形的性质和三角形全等判定来判断,举出一个反例即可证明其为假命题;
B、根据内角和外角是互余关系,将内角的变化转化为外角的变化来解答;
C、根据菱形的定义和性质进行判断;
D、根据平行线的性质进行判断.
解答:
 解:A、假命题,因为如图所示:AD=AE,AB=AC,但△ADE与△ABC不全等;
解:A、假命题,因为如图所示:AD=AE,AB=AC,但△ADE与△ABC不全等;B、假命题,因为任何多边形的外角和均为360°,则其每个外角为α=
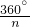 ,可见,当n增大时,α减小;
,可见,当n增大时,α减小;C、真命题,因为菱形的对角线是其对称轴,两条对角线的交点是对称中心;
D、假命题,因为两直线平行,同旁内角互补.
故选C.
点评:本题考查的是全等三角形的判定定理、多边形的内角和定理、菱形的性质及平行线的性质,涉及面较广,但较为简单.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目