题目内容
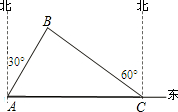 如图,一轮船以每小时20海里的速度沿正东方向航行.上午8时,该船在A处测得某灯塔位于它的北偏东30°的B处,上午12时行到C处,测得灯塔恰好在它的北偏西60°,
如图,一轮船以每小时20海里的速度沿正东方向航行.上午8时,该船在A处测得某灯塔位于它的北偏东30°的B处,上午12时行到C处,测得灯塔恰好在它的北偏西60°,分析:过B作BD⊥AC,先根据轮船的速度及行驶时间求出AC的长,再根据直角三角形的性质求出AB的长,在Rt△ABD中利用直角三角形的性质可得出AD的长,进而可得出结论.
解答: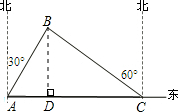 解:过B作BD⊥AC,
解:过B作BD⊥AC,
∵一轮船以每小时20海里的速度沿正东方向航行.上午8时,该船在A处出发上午12时行到C处,
∴AC=20×(12-8)=80(海里),
∵∠BAD=90°-30°=60°,∠ACB=90°-60°=30°,
∴△ABC是直角三角形,
∴AB=
AC=
×80=40(海里),
在Rt△ABD中,
∵∠BAD=90°-30°=60°,
∴∠ABD=30°,
∴AD=
AB=
×40=20(海里),
∴9时轮船离灯塔距离最近.
故答案为:9.
 解:过B作BD⊥AC,
解:过B作BD⊥AC,∵一轮船以每小时20海里的速度沿正东方向航行.上午8时,该船在A处出发上午12时行到C处,
∴AC=20×(12-8)=80(海里),
∵∠BAD=90°-30°=60°,∠ACB=90°-60°=30°,
∴△ABC是直角三角形,
∴AB=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△ABD中,
∵∠BAD=90°-30°=60°,
∴∠ABD=30°,
∴AD=
| 1 |
| 2 |
| 1 |
| 2 |
∴9时轮船离灯塔距离最近.
故答案为:9.
点评:本题考查的是解直角三角形的应用-方向角问题,根据题意作出辅助线,利用直角三角形的性质求解是解答此题的关键.

练习册系列答案
相关题目
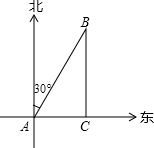 一轮船以每小时20海里的速度沿正东方向航行,上午8时,该船在A处测得某灯塔位于它的北偏东30°的B处,如图所示,上午9时行至C处,测得灯塔恰好在它的正北方向,此时它与灯塔的距离是
一轮船以每小时20海里的速度沿正东方向航行,上午8时,该船在A处测得某灯塔位于它的北偏东30°的B处,如图所示,上午9时行至C处,测得灯塔恰好在它的正北方向,此时它与灯塔的距离是 如图,一轮船以每小时20海里的速度沿正东方向航行.上午8时,该船在A处测得某灯塔位于它的北偏东30°的B处,上午12时行到C处,测得灯塔恰好在它的北偏西60°,________时轮船离灯塔距离最近.
如图,一轮船以每小时20海里的速度沿正东方向航行.上午8时,该船在A处测得某灯塔位于它的北偏东30°的B处,上午12时行到C处,测得灯塔恰好在它的北偏西60°,________时轮船离灯塔距离最近.
