题目内容
如图,已知点O为Rt△ABC斜边AB上一点,以O为圆心,OA为半径的圆与BC相切于点D,与AB相交于点E.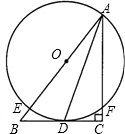
(1)试判断AD是否平分∠BAC?并说明理由.
(2)若BD=3BE,CD=3,求⊙O的半径.
分析:(1)本小题有多种证法;
方法1:作辅助线,连接OD;根据切线的性质知:OD⊥BC;由∠C=90°,可得:OD∥AC,∠1=∠2;再根据OA=OD,可得:∠2=∠3,从而得:∠1=∠3,故AD平分∠BAC;
方法2:作辅助线,连接ED;由AE为⊙O的直径,可知:∠ADE=∠3+∠AED=90;由∠C=90°,得:∠1+∠ADC=90°;再根据∠AED=∠ADC,可得:∠1=∠3,故AD平分∠BAC;
方法3,作辅助线,连接EF、DF;由AE为⊙O的直径,可知:∠AFE=90°;进而可证:EF∥BC,∠4=∠5;再根据∠4=∠3,∠1=∠5,从而可证:∠1=∠3,故AD平分∠BAC;
(2)解法1,根据切割线定理,可将AB的长求出,再根据OD∥AC,得出关于OB、OA、BD、BC的比例关系式;由此可将⊙O的半径求出;
解法2,作辅助线,过点O作OG⊥AC交AC于点G;根据OG∥BC,后同解法1.
方法1:作辅助线,连接OD;根据切线的性质知:OD⊥BC;由∠C=90°,可得:OD∥AC,∠1=∠2;再根据OA=OD,可得:∠2=∠3,从而得:∠1=∠3,故AD平分∠BAC;
方法2:作辅助线,连接ED;由AE为⊙O的直径,可知:∠ADE=∠3+∠AED=90;由∠C=90°,得:∠1+∠ADC=90°;再根据∠AED=∠ADC,可得:∠1=∠3,故AD平分∠BAC;
方法3,作辅助线,连接EF、DF;由AE为⊙O的直径,可知:∠AFE=90°;进而可证:EF∥BC,∠4=∠5;再根据∠4=∠3,∠1=∠5,从而可证:∠1=∠3,故AD平分∠BAC;
(2)解法1,根据切割线定理,可将AB的长求出,再根据OD∥AC,得出关于OB、OA、BD、BC的比例关系式;由此可将⊙O的半径求出;
解法2,作辅助线,过点O作OG⊥AC交AC于点G;根据OG∥BC,后同解法1.
解答: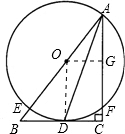 解:(1)判断:AD平分∠BAC.
解:(1)判断:AD平分∠BAC.
证明:
证法一:连接OD;
∵BC切⊙O于D,
∴OD⊥BC,
又△ABC为Rt△,且∠C=90°,
∴AC⊥BC,
∴OD∥AC,
∴∠1=∠2;
又∵OA=OD,
∴∠3=∠2,
∴∠1=∠3.
证法二:连接ED;
∵AE是⊙O直径,
∴∠ADE=90°,
∴∠3+∠AED=90°;
又∵∠C=90°,
∴∠1+∠ADC=90°,
又∵∠AED=∠ADC,
∴∠1=∠3.
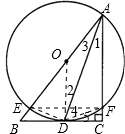
证法三:连接EF,DF;
∵AE是⊙O直径,
∴∠AFE=90°,
又∵∠ACE=90°,
∴∠AFE=∠ACB,
∴EF∥BC,
∴∠4=∠5;
又∵∠3=∠4,∠1=∠5,
∴∠1=∠3.
(2)
解法一:设BE=x,则BD=3BE=3x,
据切割线定理得BD2=BE×BA,
得AB=9x,OA=OE=4x;
又∵OD∥AC,
∴
=
,即:
=
,
∴x=
,
∴⊙O的半径为5.
解法二:
如图,过O作OG⊥AC,又AC⊥BC,OD⊥BC,
则四边形ODCG为矩形.
∴OG=CD=3,OG∥BC;
又OG∥BC,
∴
=
,
∴
=
,
∴x=
,x=0,(舍去)
∴⊙O的半径为5.
备注:本解法是在解法一得AB=9x,OA=OE=4x的基础上进行的.
 解:(1)判断:AD平分∠BAC.
解:(1)判断:AD平分∠BAC.证明:
证法一:连接OD;
∵BC切⊙O于D,
∴OD⊥BC,
又△ABC为Rt△,且∠C=90°,
∴AC⊥BC,
∴OD∥AC,
∴∠1=∠2;
又∵OA=OD,
∴∠3=∠2,
∴∠1=∠3.
证法二:连接ED;
∵AE是⊙O直径,
∴∠ADE=90°,
∴∠3+∠AED=90°;
又∵∠C=90°,
∴∠1+∠ADC=90°,
又∵∠AED=∠ADC,
∴∠1=∠3.

证法三:连接EF,DF;
∵AE是⊙O直径,
∴∠AFE=90°,
又∵∠ACE=90°,
∴∠AFE=∠ACB,
∴EF∥BC,
∴∠4=∠5;
又∵∠3=∠4,∠1=∠5,
∴∠1=∠3.
(2)
解法一:设BE=x,则BD=3BE=3x,
据切割线定理得BD2=BE×BA,
得AB=9x,OA=OE=4x;
又∵OD∥AC,
∴
| OB |
| OA |
| BD |
| CD |
| 5x |
| 4x |
| 3x |
| 3 |
∴x=
| 5 |
| 4 |
∴⊙O的半径为5.
解法二:
如图,过O作OG⊥AC,又AC⊥BC,OD⊥BC,
则四边形ODCG为矩形.
∴OG=CD=3,OG∥BC;
又OG∥BC,
∴
| OG |
| BC |
| OA |
| AB |
∴
| 3 |
| 3x+3 |
| 4x |
| 9x |
∴x=
| 5 |
| 4 |
∴⊙O的半径为5.
备注:本解法是在解法一得AB=9x,OA=OE=4x的基础上进行的.
点评:本题主要考查切线的性质及切割线定理,在解题过程中要运用相似三角形的判定等知识.

练习册系列答案
相关题目
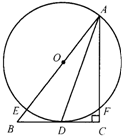 19、如图,已知点O为Rt△ABC斜边AB上一点,以O为圆心,OA为半径的圆与BC相切于点D,与AB相交于点E,与AC相交于点F.试判断AD是否平分∠BAC.并说明理由.
19、如图,已知点O为Rt△ABC斜边AB上一点,以O为圆心,OA为半径的圆与BC相切于点D,与AB相交于点E,与AC相交于点F.试判断AD是否平分∠BAC.并说明理由.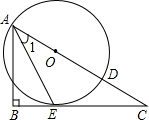 (2012•玉林)如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.
(2012•玉林)如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.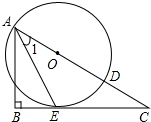 如图,已知点O为Rt△ABC斜边上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.
如图,已知点O为Rt△ABC斜边上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE. (2013•常州模拟)如图,已知点O为Rt△ABC斜边上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.
(2013•常州模拟)如图,已知点O为Rt△ABC斜边上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.