题目内容
 如图,已知点O为Rt△ABC斜边上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.
如图,已知点O为Rt△ABC斜边上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.(1)求证:AE平分∠CAB;
(2)当AE=EC,AC=3时,求⊙O的半径.
分析:(1)连接OE,则OE⊥BC,由于AB⊥BC,故可得出AB∥OE,进而可得出∠2=∠AEO,由于OA=OE,故∠1=∠AEO,进而可得出∠1=∠2;
(2)利用(1)中的结论求得∠1=∠2.所以由等腰△AEC的性质和直角三角形的两个锐角互余的性质求得3∠C=90°,则∠C=30°,所以通过解直角△OEC即可求得该圆的半径.
(2)利用(1)中的结论求得∠1=∠2.所以由等腰△AEC的性质和直角三角形的两个锐角互余的性质求得3∠C=90°,则∠C=30°,所以通过解直角△OEC即可求得该圆的半径.
解答: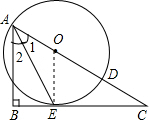 (1)证明:连接OE,
(1)证明:连接OE,
∵⊙O与BC相切于点E,
∴OE⊥BC,
∵AB⊥BC,
∴AB∥OE,
∴∠2=∠AEO.
∵OA=OE,
∴∠1=∠AEO,
∴∠1=∠2,即AE平分∠CAB;
(2)由(1)知,∠1=∠2、
∵AE=EC,
∴∠1=∠C.
∴∠1+∠2+∠C=3∠C=90°,
∴∠C=30°,
∴OE=
OC,即OE=
(3-OE),
解得,OE=1,即该圆的半径是1.
 (1)证明:连接OE,
(1)证明:连接OE,∵⊙O与BC相切于点E,
∴OE⊥BC,
∵AB⊥BC,
∴AB∥OE,
∴∠2=∠AEO.
∵OA=OE,
∴∠1=∠AEO,
∴∠1=∠2,即AE平分∠CAB;
(2)由(1)知,∠1=∠2、
∵AE=EC,
∴∠1=∠C.
∴∠1+∠2+∠C=3∠C=90°,
∴∠C=30°,
∴OE=
| 1 |
| 2 |
| 1 |
| 2 |
解得,OE=1,即该圆的半径是1.
点评:本题考查的是切线的性质、等腰三角形的性质,在解答此类题目时要熟知“若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系”.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
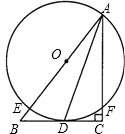
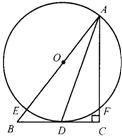 19、如图,已知点O为Rt△ABC斜边AB上一点,以O为圆心,OA为半径的圆与BC相切于点D,与AB相交于点E,与AC相交于点F.试判断AD是否平分∠BAC.并说明理由.
19、如图,已知点O为Rt△ABC斜边AB上一点,以O为圆心,OA为半径的圆与BC相切于点D,与AB相交于点E,与AC相交于点F.试判断AD是否平分∠BAC.并说明理由.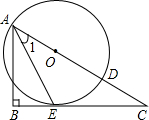 (2012•玉林)如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.
(2012•玉林)如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.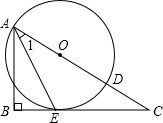 (2013•常州模拟)如图,已知点O为Rt△ABC斜边上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.
(2013•常州模拟)如图,已知点O为Rt△ABC斜边上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.