题目内容
如果关于x的一元二次方程2x2-2x+3m-1=0有两个实数根x1,x2,且它们满足不等式| x1x2 | x1+x2-3 |
分析:把两根之和与两根之积代入已知条件中,求得m的取值范围,再根据根的判别式求得m的取值范围.最后综合情况,求得m的取值范围.
解答:解:根据一元二次方程根与系数的关系知,x1+x2=1,x1•x2=
,
代入不等式得-
<1,
解得m>-1,
又∵方程有两个实数根,
∴△=b2-4ac≥0,
即(-2)2-4×2×(3m-1)≥0,
解得m≤
,
综合以上可知实数m的取值范围是-1<m≤
.
故本题答案为:-1<m≤
.
| 3m-1 |
| 2 |
代入不等式得-
| 3m-1 |
| 4 |
解得m>-1,
又∵方程有两个实数根,
∴△=b2-4ac≥0,
即(-2)2-4×2×(3m-1)≥0,
解得m≤
| 1 |
| 2 |
综合以上可知实数m的取值范围是-1<m≤
| 1 |
| 2 |
故本题答案为:-1<m≤
| 1 |
| 2 |
点评:一元二次方程根与系数的关系为,x1+x2=-
,x1•x2=
,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.
| b |
| a |
| c |
| a |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
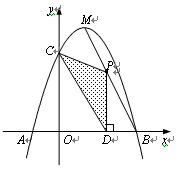
 (12分)如图,已知关于
(12分)如图,已知关于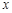 的一元二次函数
的一元二次函数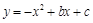 (
(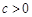 )的图象与
)的图象与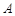 、
、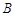 两点(点
两点(点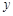 轴交于点
轴交于点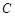 ,且
,且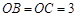 ,顶点为
,顶点为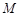 .
.
 点
点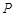 为线段
为线段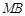 上的一个动点,过点
上的一个动点,过点 ,垂足为
,垂足为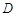 .若
.若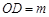 ,
,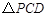 的面积为
的面积为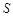 ,求
,求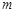 的函数关系式,并写出
的函数关系式,并写出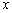 的一元二次函数
的一元二次函数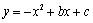 (
(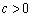 )的图象与
)的图象与 、
、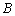 两点(点
两点(点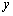 轴交于点
轴交于点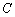 ,且
,且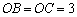 ,顶点为
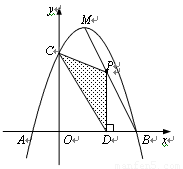
,顶点为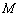 .
.
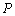 为线段
为线段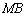 上的一个动点,过点
上的一个动点,过点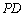 ,垂足为
,垂足为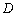 .若
.若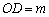 ,
, 的面积为
的面积为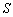 ,求
,求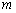 的函数关系式,并写出
的函数关系式,并写出