题目内容
 如图,将平面直角坐标系中的△AOB绕点O顺时针旋转90°得△A′OB′.已知∠AOB=60°,∠B=90°,AB=
如图,将平面直角坐标系中的△AOB绕点O顺时针旋转90°得△A′OB′.已知∠AOB=60°,∠B=90°,AB=| 3 |
分析:过点B′作B′C⊥x轴于点C,根据旋转变换的性质可得OB′=OB,再根据平角等于180°求出∠B′OC的度数,然后解直角三角形求出OC,B′C的长度,即可得解.
解答: 解:如图,过点B′作B′C⊥x轴于点C,
解:如图,过点B′作B′C⊥x轴于点C,
∵△AOB绕O点顺时针旋转90°得△A′OB′,
∴OB′=OB,∠BOB′=90°,
∵∠AOB=60°,OB=1,
∴OB′=1,
∠B′OC=180°-∠AOB-∠BOB′=180°-60°-90°=30°,
∴OC=OB′cos30°=1×
=
,
B′C=OB′sin30°=1×
=
,
∴B′的坐标为(
,
),
故选A.
 解:如图,过点B′作B′C⊥x轴于点C,
解:如图,过点B′作B′C⊥x轴于点C,∵△AOB绕O点顺时针旋转90°得△A′OB′,
∴OB′=OB,∠BOB′=90°,
∵∠AOB=60°,OB=1,
∴OB′=1,
∠B′OC=180°-∠AOB-∠BOB′=180°-60°-90°=30°,
∴OC=OB′cos30°=1×
| ||
| 2 |
| ||
| 2 |
B′C=OB′sin30°=1×
| 1 |
| 2 |
| 1 |
| 2 |
∴B′的坐标为(
| ||
| 2 |
| 1 |
| 2 |
故选A.
点评:本题考查了坐标与图形变化-旋转,用到的知识点是旋转变换的性质,解直角三角形,作辅助线构造出直角三角形是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
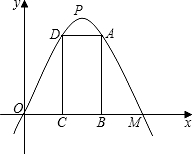 M=4,矩形ABCD的边BC在线段OM上,点A、D在抛物线上.
M=4,矩形ABCD的边BC在线段OM上,点A、D在抛物线上. 如图,在平面直角坐标中,以(5,1)为圆心,以2个单位长度为半径的⊙A交x轴于点B、C,
如图,在平面直角坐标中,以(5,1)为圆心,以2个单位长度为半径的⊙A交x轴于点B、C,

