题目内容
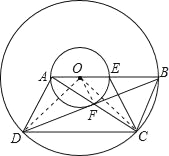
【题目】如图,在以点O为圆心的两个同心圆中,小圆直径AE的延长线与大圆交于点B,点D在大圆上,BD与小圆相切于点F,AF的延长线与大圆相交于点C,且CE⊥BD.找出图中相等的线段并证明.

【答案】见解析
【解析】试题分析:由AE是小⊙O的直径,可得OA=OE,连接OF,根据切线的性质,可得OF⊥BD,然后由垂径定理,可证得DF=BF,易证得OF∥CE,根据平行线分线段成比例定理,可证得AF=CF,继而可得四边形ABCD是平行四边形,则可得AD=BC,AB=CD.然后连接OD、OC,可证得△AOD≌△EOC,则可得BC=AD=CE=AE.
试题解析:
图中相等的线段有:OA=OE,DF=BF,AF=CF,AB=CD,BC=AD=CE=AE.
证明如下:
∵AE是小⊙O的直径,
∴OA=OE.
连接OF,
∵BD与小⊙O相切于点F,
∴OF⊥BD.
∵BD是大圆O的弦,
∴DF=BF.
∵CE⊥BD,
∴CE∥OF,
∴AF=CF.
∴四边形ABCD是平行四边形.
∴AD=BC,AB=CD.
∵CE:AE=OF:AO,OF=AO,
∴AE=EC.
连接OD、OC,
∵OD=OC,
∴∠ODC=∠OCD.
∵∠AOD=∠ODC,∠EOC=∠OEC,
∴∠AOC=∠EOC,
∴△AOD≌△EOC,
∴AD=CE.
∴BC=AD=CE=AE.

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案【题目】十八世纪瑞士数学家欧拉证明了简单多面体中项点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式。请你观察下列儿种简单多面体模型,解答下列问题:

(1)根据上面多面体模型,完成表格中的空格:
多面体 | 项点数(V) | 面数(F) | 棱数(F) |
四面体 | |||
长方体 | |||
正八面体 | |||
正十二面体 |
你发现项点数(V)、面数(F)、棱数(F)之间存在的关系式是__________________________.
(2)一个多面体的面数比顶点数小8,且有30条棱,则这多面体的顶点数是 20;
(3)某个玻璃饰品的外形是简单多面体,它的外表是由三角形和八边形两种多边形拼接而成,且有48个顶点,每个顶点处都有3条棱,设该多面体表面三角形的个数为x个,八边形的个数为y个,求x+y的值.