题目内容
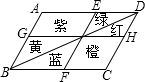 国家级历史文化名城--金华,风光秀丽,花木葱茏.某广场上一个形状是平行四边形的花坛(如图),分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果有AB∥EF∥DC,BC∥GH∥AD,那么下列说法中错误的是
国家级历史文化名城--金华,风光秀丽,花木葱茏.某广场上一个形状是平行四边形的花坛(如图),分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果有AB∥EF∥DC,BC∥GH∥AD,那么下列说法中错误的是
- A.红花,绿花种植面积一定相等
- B.紫花,橙花种植面积一定相等
- C.红花,蓝花种植面积一定相等
- D.蓝花,黄花种植面积一定相等
C
分析:根据平行四边形的性质可知GH、BD、EF把一个平行四边形分割成四个小平行四边形,我们知道,一条对角线可以把一个平行四变形的面积一分为二,据此可从图中获得S黄=S蓝,S绿=S红,S(紫+黄+绿)=S(橙+红+蓝),根据等量相减原理知S紫=S橙,依此就可找出题中说法错误的.
解答:∵AB∥EF∥DC,BC∥GH∥AD
∴GH、BD、EF把一个平行四边形分割成四个小平行四边形,
∴一条对角线可以把一个平行四变形的面积一分为二,
据此可从图中获得S黄=S蓝,S绿=S红,S(紫+黄+绿)=S(橙+红+蓝),
根据等量相减原理知S紫=S橙,
∴A、B、D说法正确,
再考查S红与S蓝显然不相等.
故选C.
点评:本题考查的是平行四变形的性质,平行四边形的一条对角线可以把平行四边形分成两个全等的三角形,两条对角线把平行四边形的面积一分为四,同时充分利用等量相加减原理解题,否则容易从直观上对S红等于S蓝产生质疑.
分析:根据平行四边形的性质可知GH、BD、EF把一个平行四边形分割成四个小平行四边形,我们知道,一条对角线可以把一个平行四变形的面积一分为二,据此可从图中获得S黄=S蓝,S绿=S红,S(紫+黄+绿)=S(橙+红+蓝),根据等量相减原理知S紫=S橙,依此就可找出题中说法错误的.
解答:∵AB∥EF∥DC,BC∥GH∥AD
∴GH、BD、EF把一个平行四边形分割成四个小平行四边形,
∴一条对角线可以把一个平行四变形的面积一分为二,
据此可从图中获得S黄=S蓝,S绿=S红,S(紫+黄+绿)=S(橙+红+蓝),
根据等量相减原理知S紫=S橙,
∴A、B、D说法正确,
再考查S红与S蓝显然不相等.
故选C.
点评:本题考查的是平行四变形的性质,平行四边形的一条对角线可以把平行四边形分成两个全等的三角形,两条对角线把平行四边形的面积一分为四,同时充分利用等量相加减原理解题,否则容易从直观上对S红等于S蓝产生质疑.

练习册系列答案
相关题目
 9、国家级历史文化名城--金华,风光秀丽,花木葱茏.某广场上一个形状是平行四边形的花坛(如图),分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果有AB∥EF∥DC,BC∥GH∥AD,那么下列说法中错误的是( )
9、国家级历史文化名城--金华,风光秀丽,花木葱茏.某广场上一个形状是平行四边形的花坛(如图),分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果有AB∥EF∥DC,BC∥GH∥AD,那么下列说法中错误的是( )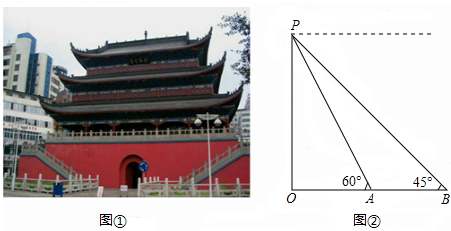
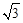 ≈1.7,结果保留整数).
≈1.7,结果保留整数).
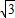 ≈1.7,结果保留整数).
≈1.7,结果保留整数).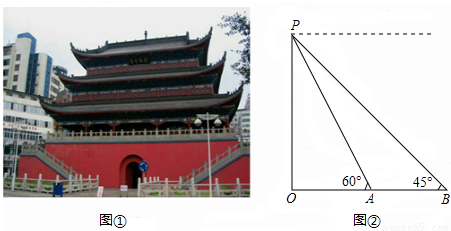
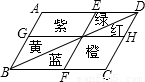 (2007•金华)国家级历史文化名城--金华,风光秀丽,花木葱茏.某广场上一个形状是平行四边形的花坛(如图),分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果有AB∥EF∥DC,BC∥GH∥AD,那么下列说法中错误的是( )
(2007•金华)国家级历史文化名城--金华,风光秀丽,花木葱茏.某广场上一个形状是平行四边形的花坛(如图),分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果有AB∥EF∥DC,BC∥GH∥AD,那么下列说法中错误的是( )