题目内容
（2010•江西）如图，以点P为圆心的圆弧与x轴交于A，B两点，点P的坐标为（4，2），点A的坐标为（2，0），则点B的坐标为 ．
【答案】分析：过点P作PM⊥AB于M，则A，B两点一定关于PM对称．即可求解．
解答：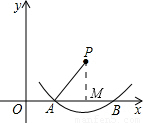
解：过点P作PM⊥AB于M，则M的坐标是（4，0）．
又∵A的坐标为（2，0），
∴OA=2，AM=OM-OA=2，
∵A，B两点一定关于PM对称．
∴MB=AM=2，
∴OB=OM+MB=4+2=6，
则点B的坐标是（6，0）．
点评：本题主要考查了圆的轴对称性，经过圆心的直线就是圆的对称轴．
解答：
解：过点P作PM⊥AB于M，则M的坐标是（4，0）．又∵A的坐标为（2，0），
∴OA=2，AM=OM-OA=2，
∵A，B两点一定关于PM对称．
∴MB=AM=2，
∴OB=OM+MB=4+2=6，
则点B的坐标是（6，0）．
点评：本题主要考查了圆的轴对称性，经过圆心的直线就是圆的对称轴．
练习册系列答案
相关题目
