题目内容
(2010•江西)如图,已知经过原点的抛物线y=-2x2+4x与x轴的另一交点为A,现将它向右平移m(m>0)个单位,所得抛物线与x轴交于C、D两点,与原抛物线交于点P.(1)求点A的坐标,并判断△PCA存在时它的形状(不要求说理);
(2)在x轴上是否存在两条相等的线段?若存在,请一一找出,并写出它们的长度(可用含m的式子表示);若不存在,请说明理由;
(3)设△CDP的面积为S,求S关于m的关系式.

【答案】分析:(1)令原抛物线的解析式中y=0,即可求得A点的坐标;
很显然P点位于线段AC的垂直平分线上,由此可判定△PAC是等腰三角形;
(2)根据平移的性质知:AO=CD=2,OC=AD=m;
(3)求△CDP的面积需要知道两个条件:底边CD及CD边上的高PH(过P作PH⊥x轴于H);
因此本题要分两种情况讨论:①0<m<2时,P点在x轴上方;②m>2时,P点位于x轴下方;
可分别表示出两种情况的CH的长即P点横坐标,根据抛物线的解析式即可得到P点的纵坐标;以CD为底,P点纵坐标的绝对值为高即可得到关于S、m的函数关系式.
解答:解:(1)令-2x2+4x=0,
得x1=0,x2=2
∴点A的坐标为(2,0)
△PCA是等腰三角形.
(2)存在.
OC=AD=m,OA=CD=2.
(3)如图,当0<m<2时,作PH⊥x轴于H,
设P(xP,yP)
∵A(2,0),C(m,0)
∴AC=2-m,
∴CH=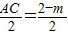
∴xP=OH=m+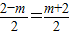
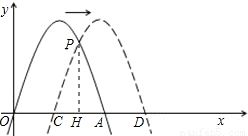
把xP=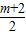 代入y=-2x2+4x,
代入y=-2x2+4x,
得yP=- m2+2
m2+2
∵CD=OA=2
∴S= CD•HP=
CD•HP= •2•(-
•2•(- m2+2)=-
m2+2)=- m2+2
m2+2
如图,当m>2时,作PH⊥x轴于H,
设P(xP,yP)
∵A(2,0),C(m,0)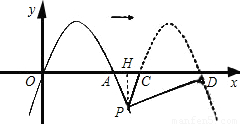
∴AC=m-2,
∴AH=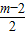
∴xP=OH=2+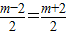
把xP=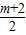 代入y=-2x2+4x,得
代入y=-2x2+4x,得
yP=- m2+2
m2+2
∵CD=OA=2
∴S= CD•HP=
CD•HP=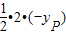 =
= m2-2.
m2-2.
点评:此题考查了二次函数图象与坐标轴交点坐标的求法、平移的性质以及三角形面积的求法等知识,需注意的是(3)题要根据m的取值范围分段讨论,以免造成漏解、错解.
很显然P点位于线段AC的垂直平分线上,由此可判定△PAC是等腰三角形;
(2)根据平移的性质知:AO=CD=2,OC=AD=m;
(3)求△CDP的面积需要知道两个条件:底边CD及CD边上的高PH(过P作PH⊥x轴于H);
因此本题要分两种情况讨论:①0<m<2时,P点在x轴上方;②m>2时,P点位于x轴下方;
可分别表示出两种情况的CH的长即P点横坐标,根据抛物线的解析式即可得到P点的纵坐标;以CD为底,P点纵坐标的绝对值为高即可得到关于S、m的函数关系式.
解答:解:(1)令-2x2+4x=0,
得x1=0,x2=2
∴点A的坐标为(2,0)
△PCA是等腰三角形.
(2)存在.
OC=AD=m,OA=CD=2.
(3)如图,当0<m<2时,作PH⊥x轴于H,
设P(xP,yP)
∵A(2,0),C(m,0)
∴AC=2-m,
∴CH=
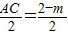
∴xP=OH=m+
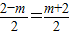

把xP=
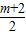 代入y=-2x2+4x,
代入y=-2x2+4x,得yP=-
 m2+2
m2+2∵CD=OA=2
∴S=
 CD•HP=
CD•HP= •2•(-
•2•(- m2+2)=-
m2+2)=- m2+2
m2+2如图,当m>2时,作PH⊥x轴于H,
设P(xP,yP)
∵A(2,0),C(m,0)

∴AC=m-2,
∴AH=
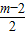
∴xP=OH=2+
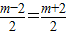
把xP=
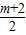 代入y=-2x2+4x,得
代入y=-2x2+4x,得yP=-
 m2+2
m2+2∵CD=OA=2
∴S=
 CD•HP=
CD•HP=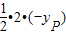 =
= m2-2.
m2-2.点评:此题考查了二次函数图象与坐标轴交点坐标的求法、平移的性质以及三角形面积的求法等知识,需注意的是(3)题要根据m的取值范围分段讨论,以免造成漏解、错解.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目



