题目内容
如果(x2-2x+m)(x-1)=0方程的三根,可作为一个三角形的三边长,则m的取值范围是
- A.
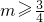
- B.
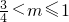
- C.
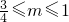
- D.
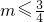
B
分析:方程(x2-2x+m)(x-1)=0的三根是一个三角形三边的长,则方程有一根是1,即方程的一边是1,另两边是方程x2-2x+m=0的两个根,根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边.则方程x2-2x+m=0的两个根设是x2和x3,一定是两个正数,且一定有|x2-x3|<1<x2+x3,结合根与系数的关系,以及根的判别式即可确定m的范围.
解答:∵方程(x2-2x+m)(x-1)=0的有三根,
∴x1=1,x2-2x+m=0有两根,
∴方程x2-2x+m=0的△=4-4m≥0,得m≤1.
又∵原方程有三根,且为三角形的三边和长.
∴有x2+x3>x1=1,|x2-x3|<x1=1,而x2+x3=2>1已成立;
当|x2-x3|<1时,两边平方得:(x2+x3)2-4x2•x3<1.
即:4-4m<1.解得,m> .
.
∴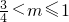 .
.
故选B.
点评:本题利用了:①一元二次方程的根与系数的关系,②根的判别式与根情况的关系判断,③三角形中两边之和大于第三边,两边之差小于第三边.
分析:方程(x2-2x+m)(x-1)=0的三根是一个三角形三边的长,则方程有一根是1,即方程的一边是1,另两边是方程x2-2x+m=0的两个根,根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边.则方程x2-2x+m=0的两个根设是x2和x3,一定是两个正数,且一定有|x2-x3|<1<x2+x3,结合根与系数的关系,以及根的判别式即可确定m的范围.
解答:∵方程(x2-2x+m)(x-1)=0的有三根,
∴x1=1,x2-2x+m=0有两根,
∴方程x2-2x+m=0的△=4-4m≥0,得m≤1.
又∵原方程有三根,且为三角形的三边和长.
∴有x2+x3>x1=1,|x2-x3|<x1=1,而x2+x3=2>1已成立;
当|x2-x3|<1时,两边平方得:(x2+x3)2-4x2•x3<1.
即:4-4m<1.解得,m>
 .
.∴
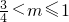 .
.故选B.
点评:本题利用了:①一元二次方程的根与系数的关系,②根的判别式与根情况的关系判断,③三角形中两边之和大于第三边,两边之差小于第三边.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
解方程
+
-3=0,如果设
=y,那么原方程可化为( )
| x2-2 |
| x |
| 2x |
| x2-2 |
| x2-2 |
| x |
| A、y2+3y+2=0 |
| B、y2-3y+2=0 |
| C、y2+3y-2=0 |
| D、y2-3y-2=0 |