题目内容
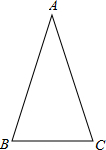 (2012•东莞)如图,在△ABC中,AB=AC,∠ABC=72°.
(2012•东莞)如图,在△ABC中,AB=AC,∠ABC=72°.(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法);
(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.
分析:(1)根据角平分线的作法利用直尺和圆规作出∠ABC的平分线即可;
(2)先根据等腰三角形的性质及三角形内角和定理求出∠A的度数,再由角平分线的定义得出∠ABD的度数,再根据三角形外角的性质得出∠BDC的度数即可.
(2)先根据等腰三角形的性质及三角形内角和定理求出∠A的度数,再由角平分线的定义得出∠ABD的度数,再根据三角形外角的性质得出∠BDC的度数即可.
解答: 解:(1)①一点B为圆心,以任意长长为半径画弧,分别交AB、BC于点E、F;
解:(1)①一点B为圆心,以任意长长为半径画弧,分别交AB、BC于点E、F;
②分别以点E、F为圆心,以大于
EF为半径画圆,两圆相交于点G,连接BG角AC于点D即可.
(2)∵在△ABC中,AB=AC,∠ABC=72°,
∴∠A=180°-2∠ABC=180°-144°=36°,
∵BD是∠ABC的平分线,
∴∠ABD=
∠ABC=
×72°=36°,
∵∠BDC是△ABD的外角,
∴∠BDC=∠A+∠ABD=36°+36°=72°.
 解:(1)①一点B为圆心,以任意长长为半径画弧,分别交AB、BC于点E、F;
解:(1)①一点B为圆心,以任意长长为半径画弧,分别交AB、BC于点E、F;②分别以点E、F为圆心,以大于
| 1 |
| 2 |
(2)∵在△ABC中,AB=AC,∠ABC=72°,
∴∠A=180°-2∠ABC=180°-144°=36°,
∵BD是∠ABC的平分线,
∴∠ABD=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BDC是△ABD的外角,
∴∠BDC=∠A+∠ABD=36°+36°=72°.
点评:本题考查的是基本作图及等腰三角形的性质,熟知角平分线的作法是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
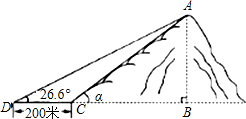 (2012•东莞)如图,小山岗的斜坡AC的坡度是tanα=
(2012•东莞)如图,小山岗的斜坡AC的坡度是tanα= (2012•东莞)如图,直线y=2x-6与反比例函数y=
(2012•东莞)如图,直线y=2x-6与反比例函数y=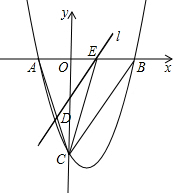 (2012•东莞)如图,抛物线y=
(2012•东莞)如图,抛物线y=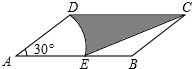 (2012•东莞)如图,在?ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是
(2012•东莞)如图,在?ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是