题目内容
 (2012•东莞)如图,抛物线y=
(2012•东莞)如图,抛物线y=| 1 |
| 2 |
| 3 |
| 2 |
(1)求AB和OC的长;
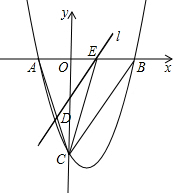
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).
分析:(1)已知抛物线的解析式,当x=0,可确定C点坐标;当y=0时,可确定A、B点的坐标,进而确定AB、OC的长.
(2)直线l∥BC,可得出△AED、△ABC相似,它们的面积比等于相似比的平方,由此得到关于s、m的函数关系式;根据题干条件:点E与点A、B不重合,可确定m的取值范围.
(3)①首先用m列出△AEC的面积表达式,△AEC、△AED的面积差即为△CDE的面积,由此可得关于S△CDE、m的函数关系式,根据函数的性质可得到S△CDE的最大面积以及此时m的值;
②过E做BC的垂线EM,这个垂线段的长即为与BC相切的⊙E的半径,可根据相似三角形△BEF、△BCO得到的相关比例线段求得该半径的值,由此得解.
(2)直线l∥BC,可得出△AED、△ABC相似,它们的面积比等于相似比的平方,由此得到关于s、m的函数关系式;根据题干条件:点E与点A、B不重合,可确定m的取值范围.
(3)①首先用m列出△AEC的面积表达式,△AEC、△AED的面积差即为△CDE的面积,由此可得关于S△CDE、m的函数关系式,根据函数的性质可得到S△CDE的最大面积以及此时m的值;
②过E做BC的垂线EM,这个垂线段的长即为与BC相切的⊙E的半径,可根据相似三角形△BEF、△BCO得到的相关比例线段求得该半径的值,由此得解.
解答:解:(1)已知:抛物线y=
x2-
x-9;
当x=0时,y=-9,则:C(0,-9);
当y=0时,
x2-
x-9=0,得:x1=-3,x2=6,则:A(-3,0)、B(6,0);
∴AB=9,OC=9.
(2)∵ED∥BC,
∴△AED∽△ABC,
∴
=(
)2,即:
=(
)2,得:s=
m2(0<m<9).
 (3)解法一:∵S△ACE=
(3)解法一:∵S△ACE=
AE•OC=
m×9=
m,
∴S△CDE=S△ACE-S△ADE=
m-
m2=-
(m-
)2+
.
∵0<m<9,
∴当m=
时,S△CDE取得最大值,最大值为
.此时,BE=AB-AE=9-
=
.
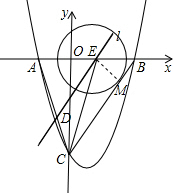
记⊙E与BC相切于点M,连接EM,则EM⊥BC,设⊙E的半径为r.
在Rt△BOC中,BC=
=
=3
.
∵∠OBC=∠MBE,∠COB=∠EMB=90°.
∴△BOC∽△BME,
∴
=
,
∴
=
,
∴r=
=
.
∴所求⊙E的面积为:π(
)2=
π.
解法二:∵S△AEC=
AE•OC=
m×9=
m,
∴S△CDE=S△AEC-S△ADE=
m-
m2=-
(m-
)2+
.
∵0<m<9,
∴当m=
时,S△CDE取得最大值,最大值为
.此时,BE=AB-AE=9-
=
.
∴S△EBC=
S△ABC=
.
如图2,记⊙E与BC相切于点M,连接EM,则EM⊥BC,设⊙E的半径为r.
在Rt△BOC中,BC=
=
.
∵S△EBC=
BC•EM,
∴
×
r=
,
∴r=
=
.
∴所求⊙E的面积为:π(
)2=
π.
| 1 |
| 2 |
| 3 |
| 2 |
当x=0时,y=-9,则:C(0,-9);
当y=0时,
| 1 |
| 2 |
| 3 |
| 2 |
∴AB=9,OC=9.
(2)∵ED∥BC,
∴△AED∽△ABC,
∴
| S△AED |
| S△ABC |
| AE |
| AB |
| s | ||
|
| m |
| 9 |
| 1 |
| 2 |
 (3)解法一:∵S△ACE=
(3)解法一:∵S△ACE=| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
∴S△CDE=S△ACE-S△ADE=
| 9 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
| 81 |
| 8 |
∵0<m<9,
∴当m=
| 9 |
| 2 |
| 81 |
| 8 |
| 9 |
| 2 |
| 9 |
| 2 |
记⊙E与BC相切于点M,连接EM,则EM⊥BC,设⊙E的半径为r.
在Rt△BOC中,BC=
| CO2+BO2 |
| 117 |
| 13 |
∵∠OBC=∠MBE,∠COB=∠EMB=90°.
∴△BOC∽△BME,
∴
| ME |
| OC |
| EB |
| CB |
∴
| r |
| 9 |
| ||
|
∴r=
| 81 | ||
2
|
27
| ||
| 26 |
∴所求⊙E的面积为:π(
| 81 | ||
2
|
| 729 |
| 52 |
解法二:∵S△AEC=
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
∴S△CDE=S△AEC-S△ADE=
| 9 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
| 81 |
| 8 |
∵0<m<9,
∴当m=
| 9 |
| 2 |
| 81 |
| 8 |
| 9 |
| 2 |
| 9 |
| 2 |
∴S△EBC=
| 1 |
| 2 |
| 81 |
| 4 |
如图2,记⊙E与BC相切于点M,连接EM,则EM⊥BC,设⊙E的半径为r.
在Rt△BOC中,BC=
| 92+62 |
| 117 |
∵S△EBC=
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 117 |
| 81 |
| 4 |
∴r=
| 81 | ||
2
|
27
| ||
| 26 |
∴所求⊙E的面积为:π(
| 81 | ||
2
|
| 729 |
| 52 |
点评:该题主要考查了二次函数的性质、相似三角形的性质、图形面积的求法等综合知识.在解题时,要多留意图形之间的关系,有些时候将所求问题进行时候转化可以大大的降低解题的难度.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
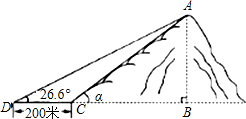 (2012•东莞)如图,小山岗的斜坡AC的坡度是tanα=
(2012•东莞)如图,小山岗的斜坡AC的坡度是tanα= (2012•东莞)如图,直线y=2x-6与反比例函数y=
(2012•东莞)如图,直线y=2x-6与反比例函数y=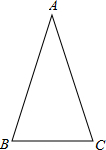 (2012•东莞)如图,在△ABC中,AB=AC,∠ABC=72°.
(2012•东莞)如图,在△ABC中,AB=AC,∠ABC=72°.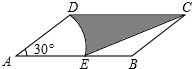 (2012•东莞)如图,在?ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是
(2012•东莞)如图,在?ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是