题目内容
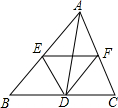
 如图,点D、E、F分别是△ABC三边AB、BC、AC的中点,则△DEF的周长是△ABC周长的( )
如图,点D、E、F分别是△ABC三边AB、BC、AC的中点,则△DEF的周长是△ABC周长的( )分析:根据D、E、F分别是AB、AC、BC的中点,可以判断DF、FE、DE为三角形中位线,利用中位线定理求出DF、FE、DE与AB、BC、CA的长度关系即可解答.
解答:解:∵D、E、F分别是AB、BC、AC的中点,
∴ED、FE、DF为△ABC中位线,
∴DF=
BC,FE=
AB,DE=
AC;
∴DF+FE+DE=
BC+
AB+
AC=
(AB+BC+CA);
即△DEF是△ABC的周长的
.
故选A.
∴ED、FE、DF为△ABC中位线,
∴DF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴DF+FE+DE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即△DEF是△ABC的周长的
| 1 |
| 2 |
故选A.
点评:本题考查了三角形的中位线定理,根据中点判断出中位线,再利用中位线定理是解题的基本思路.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
 如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )
如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )| A、EF与AD互相平分 | ||
B、EF=
| ||
| C、AD平分∠BAC | ||
| D、△DEF∽△ACB |
 如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )
如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )| A、AD平分∠BAC | ||
B、EF=
| ||
| C、EF与AD互相平分 | ||
| D、△DFE是△ABC的位似图形 |
 5、如图,点D、E、F分别是△ABC的边AB、BC、AC的中点,连接DE、EF,要使四边形ADEF为正方形,还需增加条件:
5、如图,点D、E、F分别是△ABC的边AB、BC、AC的中点,连接DE、EF,要使四边形ADEF为正方形,还需增加条件: 如图,点D,E,F分别是△ABC的三边AB,AC,BC上的中点,如果△ABC的面积是18cm2,则△DBF的面积是
如图,点D,E,F分别是△ABC的三边AB,AC,BC上的中点,如果△ABC的面积是18cm2,则△DBF的面积是