题目内容
如图,菱形ABCD中,AB=10,sinA=
,点E在AB上,AE=4,过点E作EF∥AD,交CD于F,点P从点A出发以1个单位/s的速度沿着线段AB向终点B运动,同时点Q从点E出发也以1个单位/s的速度沿着线段EF向终点F运动,设运动时间为t(s).
(1)填空:当t=5时,PQ=
(2)当BQ平分∠ABC时,直线PQ将菱形的周长分成两部分,求这两部分的比;
(3)以P为圆心,PQ长为半径的⊙P是否能与直线AD相切?如果能,求此时t的值;如果不能,说明理由.

| 4 |
| 5 |
(1)填空:当t=5时,PQ=
2
| 5 |
2
;| 5 |
(2)当BQ平分∠ABC时,直线PQ将菱形的周长分成两部分,求这两部分的比;
(3)以P为圆心,PQ长为半径的⊙P是否能与直线AD相切?如果能,求此时t的值;如果不能,说明理由.

分析:(1)过点P作PM⊥EF,垂足为M,利用锐角三角函数求得PM的长,然后利用勾股定理求得EM的长,再利用勾股定理求得PQ的长即可;
(2)根据题意画出图象,结合图形和已知条件证得△EPQ∽△FMQ,进而求得MC的长,然后求得菱形的周长被分成两部分,并据此求得两部分的比值;
(3)过P作PH⊥AD于H,并利用勾股定理PQ2=(
t)2+(4-
t)2后求得t的值即可.
(2)根据题意画出图象,结合图形和已知条件证得△EPQ∽△FMQ,进而求得MC的长,然后求得菱形的周长被分成两部分,并据此求得两部分的比值;
(3)过P作PH⊥AD于H,并利用勾股定理PQ2=(
| 4 |
| 5 |
| 2 |
| 5 |
解答:解:(1)根据题意画出图形,如图所示:
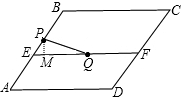
过点P作PM⊥EF,垂足为M,
由题意可知AE=4,AP=EQ=5,则EP=1,
∵EF∥AD,
∴∠BEF=∠A,即sin∠BEF=sinA=
,
即
=
,则PM=
,
根据勾股定理得:EM=
,
则MQ=5-
=
,
在直角三角形PQM中,根据勾股定理得:
PQ=
=2
;
(2)根据题意画出图形,如图所示:
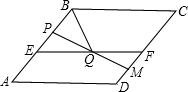
∵BQ平分∠ABC,
∴∠EBQ=∠CBQ,
又∵BC∥EF,
∴∠CBQ=∠EQB,
∴∠EBQ=∠EQB,
∴EB=EQ=10-4=6,
则t=6,AP=6,
∴BP=4,QF=4,
设PQ交CD于点M,
∵AB∥CD,
∴∠EPQ=∠FMQ,∠PEQ=∠MFQ,
∴△EPQ∽△FMQ,
∴
=
,即
=
,
∴FM=
,
则MD=4-
=
,MC=
,
则直线PM分菱形分成的两部分的周长分别为AP+AD+MD和PB+BC+CM,
即菱形的周长被分为
和
,
所以这两部分的比为7:8;
(3)过P作PH⊥AD于H,交EF于G点,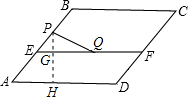
则PH=
t,PE=t-4,PG=
(t-4),EG=
(t-4),
∴GQ=t-EG=
t+
,
PQ2=PG2+GQ2=(
t-
)2+(
t+
)2,
由题意可得方程(
t)2=(
t-
)2+(
t+
)2,
解得:t=10.

过点P作PM⊥EF,垂足为M,
由题意可知AE=4,AP=EQ=5,则EP=1,
∵EF∥AD,
∴∠BEF=∠A,即sin∠BEF=sinA=
| 4 |
| 5 |
即
| PM |
| EP |
| 4 |
| 5 |
| 4 |
| 5 |
根据勾股定理得:EM=
| 3 |
| 5 |
则MQ=5-
| 3 |
| 5 |
| 22 |
| 5 |
在直角三角形PQM中,根据勾股定理得:
PQ=
(
|
| 5 |
(2)根据题意画出图形,如图所示:

∵BQ平分∠ABC,
∴∠EBQ=∠CBQ,
又∵BC∥EF,
∴∠CBQ=∠EQB,
∴∠EBQ=∠EQB,
∴EB=EQ=10-4=6,
则t=6,AP=6,
∴BP=4,QF=4,
设PQ交CD于点M,
∵AB∥CD,
∴∠EPQ=∠FMQ,∠PEQ=∠MFQ,
∴△EPQ∽△FMQ,
∴
| EP |
| FM |
| EQ |
| QF |
| 2 |
| FM |
| 6 |
| 4 |
∴FM=
| 4 |
| 3 |
则MD=4-
| 4 |
| 3 |
| 8 |
| 3 |
| 22 |
| 3 |
则直线PM分菱形分成的两部分的周长分别为AP+AD+MD和PB+BC+CM,
即菱形的周长被分为
| 56 |
| 3 |
| 64 |
| 3 |
所以这两部分的比为7:8;
(3)过P作PH⊥AD于H,交EF于G点,

则PH=
| 4 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
∴GQ=t-EG=
| 2 |
| 5 |
| 12 |
| 5 |
PQ2=PG2+GQ2=(
| 4 |
| 5 |
| 16 |
| 5 |
| 2 |
| 5 |
| 12 |
| 5 |
由题意可得方程(
| 4 |
| 5 |
| 4 |
| 5 |
| 16 |
| 5 |
| 2 |
| 5 |
| 12 |
| 5 |
解得:t=10.
点评:本题考查了菱形的性质、切线的判定及性质及解直角三角形的知识,解题的关键是正确地作出图形.

练习册系列答案
相关题目
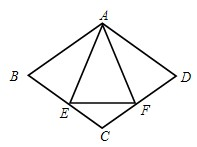 26、已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.
26、已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF. 如图,菱形ABCD中,∠A=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿B→C→D向终点D运动.同时动点Q从点A出发,以相同的速度沿A→D→B向终点B运动,运动的时间为x秒,当点P到达点D时,点P、Q同时停止运动,设△APQ的面积为y,则反映y与x的函数关系的图象是( )
如图,菱形ABCD中,∠A=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿B→C→D向终点D运动.同时动点Q从点A出发,以相同的速度沿A→D→B向终点B运动,运动的时间为x秒,当点P到达点D时,点P、Q同时停止运动,设△APQ的面积为y,则反映y与x的函数关系的图象是( )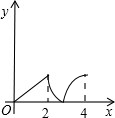
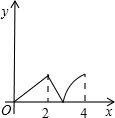
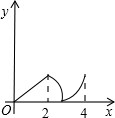
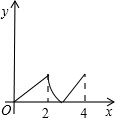
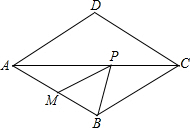 如图,菱形ABCD中,∠BAD=60°,M是AB的中点,P是对角线AC上的一个动点,若AB长为2
如图,菱形ABCD中,∠BAD=60°,M是AB的中点,P是对角线AC上的一个动点,若AB长为2 如图:菱形ABCD中,E是AB的中点,且CE⊥AB,AB=6cm.
如图:菱形ABCD中,E是AB的中点,且CE⊥AB,AB=6cm. 如图,菱形ABCD中,∠ADC=120°,AB=10,
如图,菱形ABCD中,∠ADC=120°,AB=10,