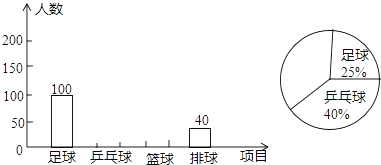
题目内容
【题目】已知二次函数y=ax2-4ax+a2+2(a<0)图像的顶点G在直线AB上,其中A(![]() ,0)、B(0,3),
,0)、B(0,3),
对称轴与x轴交于点E.
(1)求二次函数y=ax2-4ax+a2+2的关系式;
(2)点P在对称轴右侧的抛物线上,且AP平分四边形GAEP的面积,求点P坐标;
(3)在x轴上方,是否存在整数m,使得当![]() < x ≤
< x ≤![]() 时,抛物线y随x增大而增大,若存在,求出所有满足条件的m值;若不存在,请说明理由.
时,抛物线y随x增大而增大,若存在,求出所有满足条件的m值;若不存在,请说明理由.
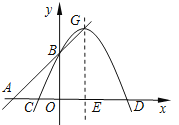
【答案】(1)二次函数关系式为y=-x2+4x+3;
(2)P(![]() ,
, ![]() ),
),
(3)m取-2、-1
【解析】解(1)由A(-![]() ,0)、B(0,3),可设直线AB:y=kx+3,
,0)、B(0,3),可设直线AB:y=kx+3,
从而得,k=2, ∴y=2x+3,
抛物线y=ax2-4ax+a2+2的顶点G(2,a2-4a+2),
点G在直线AB上,∴ a2-4a+2=4+3,∴a=-1,a=5(舍去),
二次函数关系式为y=-x2+4x+3.
(2)∵AP平分四边形GAEP的面积, ∴2S△AEP=S四边形GAEP,
设P(t,-t2+4t+3),
∴ 2×![]() (2+
(2+![]() )(-t2+4t+3)=
)(-t2+4t+3)=![]() ×7×(2+
×7×(2+![]() )+
)+![]() ×7×(t-2)
×7×(t-2)
∴ 2t2-6 t-3=0,∴t1=![]() , t2=
, t2=![]() (舍去)∴P(
(舍去)∴P(![]() ,
, ![]() ),
),
(3)抛物线与x轴交点C(2-![]() ,0),D(2+
,0),D(2+![]() ,0),
,0),
在x轴上方,抛物线y随x增大而减大,则2-![]() <x≤2,
<x≤2,
又∵![]() < x≤
< x≤![]() ,
,
∴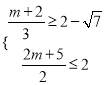 ,得:4-3
,得:4-3![]() ≤m≤-
≤m≤-![]() ,
,
∵整数m为整数,∴m为-3,-2、-1.
又∵![]() <
<![]() ,m>-
,m>-![]() .
.
∴m取-2、-1.

练习册系列答案
相关题目