题目内容
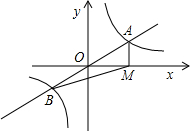 如图,直线y=mx与双曲线y=
如图,直线y=mx与双曲线y=| k |
| x |
分析:先设出A点坐标,再根据反比例函数与正比例函数的特点得出B点坐标,根据S△ABM=3即可得出k的值.
解答:解:设A(x,y),
∵反比例函数与正比例函数的图象均关于原点对称,
∴A、B两点关于原点对称,
∴B(-x,-y),
∵AM⊥x轴,
∴S△ABM=
y•2x=3,解得xy=3,
∴k=xy=3.
故选A.
∵反比例函数与正比例函数的图象均关于原点对称,
∴A、B两点关于原点对称,
∴B(-x,-y),
∵AM⊥x轴,
∴S△ABM=
| 1 |
| 2 |
∴k=xy=3.
故选A.
点评:本题考查的是反比例函数系数k的几何意义,熟知反比例函数与正比例函数的图象均关于原点对称是解答此题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
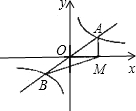 如图,直线y=mx与双曲线y=
如图,直线y=mx与双曲线y=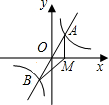 如图,直线y=mx与双曲线y=
如图,直线y=mx与双曲线y=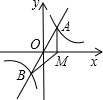 如图,直线y=mx与双曲线
如图,直线y=mx与双曲线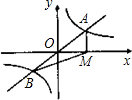 如图,直线y=mx与双曲线y=
如图,直线y=mx与双曲线y=